Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = 2a, SA vuông góc với đáy. Cạnh bên SD tạo với đáy một góc 60⁰. Gọi M, N lần lượt là trung điểm của AB, CD.
1. Tính khoảng cách từ A đến (SBN)
2. Tính khoảng cách từ M đến (SBN)
3. Tính khoảng cách từ D đến (SBN)
Joli Talentueux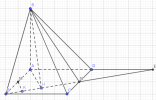
a) [imath](SD,(ABCD))=\widehat{SDA}[/imath]
[imath]\tan \widehat{SDA}=\tan 60^\circ= \dfrac{SA}{AD}=\sqrt3\Rightarrow SA=2a\sqrt3[/imath]
Kẻ [imath]AH\bot BN, MK\bot BN[/imath]
[imath]\Rightarrow MB=\dfrac{AB}2=\dfrac{a}2; MN=AD=2a[/imath]
[imath]\Rightarrow \dfrac{1}{MK^2}=\dfrac{1}{MB^2}+\dfrac{1}{MN^2}\Rightarrow MK=\dfrac{2a\sqrt{17}}{17}[/imath]
[imath]\Rightarrow AH=2MK=\dfrac{4a\sqrt{17}}{17}[/imath] (AB=2BM)
Ta có: [imath]\dfrac{1}{d(A,(SBN))^2}=\dfrac{1}{AH^2}+\dfrac{1}{SA^2}[/imath]
[imath]\Rightarrow d(A,(SBN))=\dfrac{4a\sqrt{165}}{55}[/imath]
b) [imath]\dfrac{MB}{AB}=\dfrac{1}2\Rightarrow d(M,(SBN))=\dfrac{1}2d(A,(SBN))=\dfrac{2a\sqrt{165}}{55}[/imath]
c) Gọi [imath]E=AD\cap BN[/imath]
[imath]\dfrac{ND}{AB}=\dfrac{1}2=\dfrac{DE}{AE}[/imath]
[imath]\Rightarrow d(D,(SBN))=\dfrac{1}2d(A,(SBN))=\dfrac{2a\sqrt{165}}{55}[/imath]
Có gì khúc mắc em hỏi lại nha
Ngoài ra, em xem thêm tại
Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.


