[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
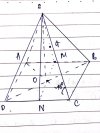
Cho hình chóp [imath]S.ABCD[/imath] có đáy [imath]ABCD[/imath] là hình vuông tâm [imath]O[/imath] cạnh bằng [imath]2a[/imath]. [imath]SO \perp (ABCD)[/imath], cạnh bên [imath]SC[/imath] tạo với đáy một góc [imath]45^o[/imath], [imath]G[/imath] là trọng tâm tam giác [imath]SAB.[/imath]
Tính khoảng cách từ điểm [imath]G[/imath] đến mặt phẳng [imath](SCD)[/imath]
Tính khoảng cách từ điểm [imath]G[/imath] đến mặt phẳng [imath](SCD)[/imath]
Last edited by a moderator: