[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
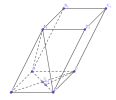
Cho hình lăng trụ [imath]ABCD.A_{1}B_{1}C_{1}D_{1}[/imath] có đáy là hình chữ nhật với [imath]AB=a, AD= \sqrt{3}[/imath]. Hình chiếu vuông góc của [imath]A_{1}[/imath] lên [imath](ABCD)[/imath] trùng với giao điểm của[imath]AC[/imath] và [imath]BD[/imath]. Tính khoàng cách từ [imath]B_{1}[/imath] đến mp [imath](A_{1}BD)[/imath]

Em còn câu này không lm đc, mng giúp em với ạ

Em còn câu này không lm đc, mng giúp em với ạ