- 7 Tháng tám 2018
- 2,945
- 7,443
- 621
- 19
- Lào Cai
- Trường THPT số 1 Lào Cai
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
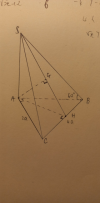
Cho hình chóp [imath]S.ABC[/imath] có đáy là tam giác vuông tại [imath]A[/imath], [imath]AC = 2a; BC =4a[/imath]. Cạnh bên [imath]SA \perp (ABC)[/imath], đường thẳng [imath]SB[/imath] tạo với mặt phẳng [imath](ABC)[/imath] góc [imath]60^o[/imath]
a) Xác định và tính khoảng cách từ [imath]S[/imath] đến [imath](ABC)[/imath]
b) Xác định và tính khoảng cách từ [imath]A[/imath] đến [imath](SBC)[/imath]
Giúp em với ạ, trình bày rõ ràng giúp em ạ
a) Xác định và tính khoảng cách từ [imath]S[/imath] đến [imath](ABC)[/imath]
b) Xác định và tính khoảng cách từ [imath]A[/imath] đến [imath](SBC)[/imath]
Giúp em với ạ, trình bày rõ ràng giúp em ạ
Attachments
Last edited by a moderator: