P
psdyf1
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Bài 1 : Cho hình thang cân ABCD ( AB//CD , AB>CD) có góc A+ góc B =1/2 (C+B) . Đường chéo AC vuông góc với cạnh bên BC .
a) Tính các góc của hình thang
b) Chứng minh AC là phân giác của góc DAB
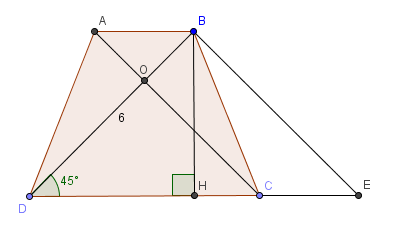
Bài 2 : Cho hình thang cân ABCD ( AB//CD) có góc BDC bằng 45 độ . Gọi O là giao điểm của AC và BD.
a) CM tam giác DOC vuông cân
b) Tính diện tích hình thang ABCD biết BD = 6 cm
Giải theo cách lớp 8 giùm mình nhé
a) Tính các góc của hình thang
b) Chứng minh AC là phân giác của góc DAB
Bài 2 : Cho hình thang cân ABCD ( AB//CD) có góc BDC bằng 45 độ . Gọi O là giao điểm của AC và BD.
a) CM tam giác DOC vuông cân
b) Tính diện tích hình thang ABCD biết BD = 6 cm
Giải theo cách lớp 8 giùm mình nhé
Last edited by a moderator: