[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
 Cùng nhau ôn tập lại chương IV hình học 8 các bạn nhé. Bắt đầu từ hình hộp chữ nhật nha. Gét gô
Cùng nhau ôn tập lại chương IV hình học 8 các bạn nhé. Bắt đầu từ hình hộp chữ nhật nha. Gét gôHÌNH HỘP CHỮ NHẬT
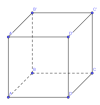
- Hình hộp chữ nhật có: 6 mặt, 8 đỉnh, 12 cạnh.
- Hình lập phương là hình hộp chữ nhật có 6 mặt là hình vuông.
II. Tính chất
+ Hai đường thẳng phân biệt trong không gian có các vị trí:
- Cắt nhau nếu có một điểm chung, chẳng hạn AB cắt BC.
- Song song nếu cùng nằm trong một mặt phẳng và không có điểm chung, chẳng hạn AB //CD.
- Chéo nhau nếu không cùng nằm trong một mặt phẳng nào, chẳng hạn AB và CC′.
+ Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.
+ Nếu đường thẳng [imath](\alpha)[/imath] không nằm trong mặt phẳng [imath](P)[/imath] và song song với một đường thẳng của [imath](P)[/imath] thì đường thẳng [imath](\alpha)[/imath] song song với [imath](P)[/imath].
+ Nếu mặt phẳng [imath](Q)[/imath] chứa hai đường thẳng cắt nhau và chúng cùng song song với [imath](P)[/imath] thì [imath](Q)//(P)[/imath]
+ Hai mặt phẳng phân biệt có các vị trí:
- Song song, nếu chúng không có điểm chung nào.
- Cắt nhau, nếu tồn tại một điểm chung, khi đó chúng cắt nhau theo một đường thẳng đi qua điểm chung đó.
- Diện tích xung quanh hình hộp chữ nhật: [imath]2(ab+bc+ca)[/imath]
[imath]\Rightarrow[/imath] Diện tích xung quanh hình lập phưng là: [imath]6a^2[/imath]
- Thể tích hình hộp chữ nhật là: [imath]abc[/imath]
[imath]\Rightarrow[/imath] Thể tích hình lập phương là [imath]a^3[/imath]
III. Các dạng toán thường gặp
Dạng toán 1: Nhận biết quan hệ vuông góc giữa đường thẳng và mặt phẳng trong hình hộp chữ nhật
Ví dụ: Cho hình hộp chữ nhật ABCD.EFGH như hình vẽ.

a) Kể tên các đường thẳng được vẽ trên hình và vuông góc vói BF.
b) Kể tên ba cặp mặt phẳng vuông góc với nhau.
c) AC có vuông góc với DH không? Vì sao?
d) Chứng minh tam giác AEG vuông tại E. Từ đó chứng minh [imath]AG=\sqrt{AE^2+EF^2+EH^2}[/imath] (AG được gọi là đường chéo hình hộp chữ nhật).
Hướng Dẫn:
a) Các đường thẳng vuông góc với BF là: AB, BC, CD, DA, AC, EF, FG, GH, HE và FH.
b) (ABCD) và (BCGF), (CDHG) và (EFGH), (ADHE) và (ABCD)
Lưu ý: HS có thể liệt kê tên các cặp mặt phẳng khác.
c) [imath]AC\bot DH[/imath] vì [imath]DH\bot (ABCD)[/imath]
d) Ta có: [imath]AE\bot (EFGH)[/imath] nên [imath]AE\bot EG[/imath]. Từ đó, theo định lý Pitago, ta được
[imath]AG^2=AE^2+EG^2=AE^2+EF^2+EH^2[/imath]
Dạng 2. Tính toán thể tích và các số liệu liên quan đến cạnh và mặt của hình hộp chữ nhật
Ví dụ: Cho biết một bể bơi tiêu chuẩn có chiều dài 50 m, chiều rộng 25 m và cao 2,3 m. Người ta bơm nước vào bể sao cho nước cách mép bể 0,5 m.
a) Tính thể tích nước trong bể.
b) Tính thể tích phần bể không chứa nước.
Hướng dẫn
a) Nước trong bể tạo thành một hình hộp chữ nhật có chiều dài 50m, chiều rộng 25m và chiều cao 1,8m.
Từ đó ta tính được thể tích nước trong bể [imath]V_1 = 2250m^3[/imath].
b) Cách 1: Phần bể không chứa nước tạo thành một hình hộp chữ nhật có chiều dài 50m, chiều rộng 25m và chiều cao 0,5m. Từ đó tính được [imath]V_2 = 625m^3[/imath].
Cách 2: Thể tích của cả bể là [imath]V = 2872m^3[/imath]. Từ đó [imath]V_2 = 625m^3[/imath].
VI. BÀI TẬP VẬN DỤNG
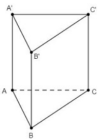
1. Cho hình lập phương ABCD.A'B'C'D'
a) Nêu vị trí tương đối của các cặp đường thẳng BC' và A'D'; DD' và AB; AA’ và A’C'.
b) Chứng minh A'C' vuông góc với (BB'D'). Từ đó chứng minh A'C' vuông góc BD'.
c) Chứng minh [imath]BO=\sqrt{BB'^2+\dfrac{1}4(AB^2+BC^2)}[/imath]
2. Một hình hộp chữ nhật có thể tích bằng 60 và diện tích toàn phần bằng 94 . Tính chiều rộng, chiều dài của hình hộp chữ nhật biết chiều cao bằng 4cm.
 Hãy cùng nhau thử sức mình bằng các bài tập vận dụng các em nhé <3
Hãy cùng nhau thử sức mình bằng các bài tập vận dụng các em nhé <3