C
cocute1403
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
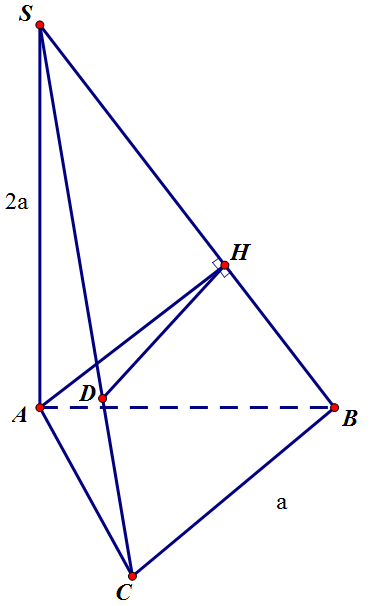
Cho hình chóp $SABC$ có đáy $(ABC)$ vuông cân tại $C$. mp$(SAB)$ và $(SAC)$ vuông góc với $(SBC)$. cho $SA=2a$, $BC=a$. xác định góc giữa mp$(SBC)$ và mp$(SAB)$?
Mình nghĩ không ra. thầy cô/các bạn có rảnh thì vào giúp mình chút nhé!
Mình nghĩ không ra. thầy cô/các bạn có rảnh thì vào giúp mình chút nhé!