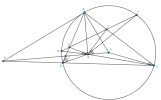
Nếu để ý kỹ thì ta thấy điểm [imath]X[/imath] là điểm [imath]A[/imath]-Dumpty của [imath]\Delta ABC[/imath] nên ta sẽ chứng minh điều trên.
Ta sẽ cần [imath]2[/imath] điều kiện là [imath]X[/imath] nằm trên đường đối trung từ đỉnh [imath]A[/imath] của [imath]\Delta ABC[/imath] và [imath]\widehat{OXA}=90^o[/imath].
Xét cực và đối cực với đường tròn [imath](O)[/imath].
Nhận thấy [imath]P[/imath] là cực của đường thẳng [imath]AX[/imath] và [imath]P[/imath] nằm trên [imath]BC[/imath] nên đường thẳng [imath]AX[/imath] phải đi qua cực của [imath]BC[/imath].
Tức là [imath]AX[/imath] đi qua giao điểm [imath]2[/imath] tiếp tuyến của [imath]B,C[/imath] với [imath](O)[/imath] hay [imath]AX[/imath] là đường đối trung của [imath]\Delta ABC[/imath].
Vậy [imath]X[/imath] là điểm [imath]A[/imath]-Dumpty của [imath]\Delta ABC[/imath].
Chứng minh được điểm Dumpty thì sẽ có một số tính chất từ điểm [imath]X[/imath], nhưng anh sẽ chỉ dùng tính chất định nghĩa của điểm Dumpty là [imath]\widehat{ABX}=\widehat{XAC}[/imath] và [imath]\widehat{ACX}=\widehat{XAB}[/imath]
Khi đó dễ thấy [imath]XE \perp AB, XF \perp AC[/imath].
Từ đó [imath]AEXF[/imath] nội tiếp và [imath](XEF)[/imath] tiếp xúc [imath]OX[/imath]. Ta chỉ cần chứng minh [imath](XEF)[/imath] và [imath](XKL)[/imath] tiếp xúc tại [imath]X[/imath] nữa là được.
Điều này tương đương với việc chứng minh [imath]XK,XL[/imath] đẳng giác với nhau trong [imath]\widehat{EXF}[/imath]
[imath]\Leftrightarrow \dfrac{EK \cdot EL}{FK \cdot FL}=\dfrac{XE^2}{XF^2}[/imath] (2 điều tương đương trên là do tính chất của đường đẳng giác)
Mặt khác, [imath]EK \cdot EL=AE \cdot EB, FK \cdot FL=AF \cdot FC[/imath] nên ta sẽ chứng minh [imath]\dfrac{AE}{AF} \cdot \dfrac{EB}{FC}=\dfrac{XE^2}{XF^2}[/imath]
Nhận thấy [imath]\dfrac{XE}{XF}=\dfrac{XE}{AX} : \dfrac{XF}{AX}=\dfrac{\sin \widehat{BAX}}{\sin \widehat{CAX}}[/imath]
và [imath]\dfrac{XB}{XC}=\dfrac{XB}{AX} \cdot \dfrac{AX}{XC}=\dfrac{\sin \widehat{BAX}}{\sin \widehat{ABX}} \cdot \dfrac{\sin \widehat{ACX}}{\sin \widehat{CAX}}=(\dfrac{\sin \widehat{BAX}}{\sin \widehat{CAX}})^2[/imath]
[imath]\Rightarrow \dfrac{XE^2}{XF^2}=\dfrac{XB}{XC}[/imath]
Ta cần chứng minh [imath]\dfrac{AE}{AF} \cdot \dfrac{EB}{FC}=\dfrac{XB}{XC} \Leftrightarrow \dfrac{AE}{AF}=\dfrac{CF}{XC} : \dfrac{EB}{BX}[/imath]
Nhận thấy [imath]\dfrac{AE}{AF}=\widehat{AE}{AX} : \dfrac{AF}{AX}=\dfrac{\cos \widehat{BAX}}{\cos \widehat{CAX}}[/imath]
[imath]\dfrac{CF}{XC}=\cos \widehat{XCA}=\cos \widehat{BAX}, \dfrac{EB}{BX}=\cos \widehat{XBA}=\cos \widehat{CAX}[/imath]
Từ đây ta có đpcm.
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé ^^ Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại đây nhé
Đề thi ôn tập chọn HSGQG
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
