[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
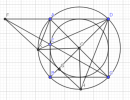
Cho hình veông [imath]A B C D[/imath] tâm [imath]O[/imath]. Lấy điểm [imath]E[/imath] trên đoạn [imath]A B[/imath] (E khác [imath]B[/imath] và [imath]A)[/imath], goi [imath]F[/imath] là giao điểm của [imath]\mathrm{CE}[/imath] và [imath]\mathrm{DA}[/imath], đường thẳng [imath]\mathrm{DE}[/imath] cát đuồng tròn ( [imath]\mathrm{O} ; \mathrm{OA})[/imath] tại điểm [imath]\mathrm{K}[/imath] (K khác [imath]\mathrm{D})[/imath]. Qua [imath]\mathrm{K}[/imath] kè tiép tuyyến [imath]\mathrm{KH}[/imath] với đường tròn [imath]\left(\mathrm{O} ; \frac{\mathrm{AB}}{2}\right)[/imath] (H thuộc [imath](\mathrm{O} ; \mathrm{OA})[/imath] và nằm khác phía với [imath]\mathrm{D}[/imath] qua [imath]\left.\mathrm{FC}\right)[/imath].
a) Chứng minh rằng từ giác KHDA là hình thang cân.
b) Chừng minh rằng [imath]\mathrm{F}, \mathrm{K}[/imath], [imath]\mathrm{H}[/imath] thẳng hàng.
Giúp em hai bài 6 với ạ!!!!!!!!!!!!!
a) Chứng minh rằng từ giác KHDA là hình thang cân.
b) Chừng minh rằng [imath]\mathrm{F}, \mathrm{K}[/imath], [imath]\mathrm{H}[/imath] thẳng hàng.
Giúp em hai bài 6 với ạ!!!!!!!!!!!!!