[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
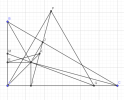
Cho tam giác ABC vuông tại A. Các tia phân giác của góc B và góc C cắt nhau tại I. Gọi D,E,F lần lượt là hình chiếu vuông góc của I lên BC;AB;AC.
1.Chứng minh: Tứ giác AEIF là hình vuông và ID=IE=IF
2. Tia AI cắt DF tại K a, Chứng minh rằng tam giác AIB đồng dạng với tam giác AFK b, Qua A kẻ đường thẳng vuông góc với BC, đường thẳng này cắt DF tại P. Gọi M là trung điẻm của AB. Tia MI cắt cạnh Ac tai Q. CHứng minh tam giác APQ cân.
3. Khi BC cố định, điểm A di chuyển nhưng vẫn thảo mãn góc BAC = 90 độ và đoạn AI không đổi bằng a căn 2. Tìm vị trí của A để chu vi AMQ nhỏ nhát
1.Chứng minh: Tứ giác AEIF là hình vuông và ID=IE=IF
2. Tia AI cắt DF tại K a, Chứng minh rằng tam giác AIB đồng dạng với tam giác AFK b, Qua A kẻ đường thẳng vuông góc với BC, đường thẳng này cắt DF tại P. Gọi M là trung điẻm của AB. Tia MI cắt cạnh Ac tai Q. CHứng minh tam giác APQ cân.
3. Khi BC cố định, điểm A di chuyển nhưng vẫn thảo mãn góc BAC = 90 độ và đoạn AI không đổi bằng a căn 2. Tìm vị trí của A để chu vi AMQ nhỏ nhát