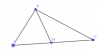
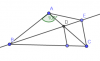
Bài 1: Trên các cạnh Ox và Oy của góc xOy, lấy các điểm A và B sao cho OA = OB. Tia phân giác của các góc xOy cắt AB ở C. Chứng minh rằng:
C là trung điểm của AB
GIẢI:
Gọi giao điểm của OC và AB là I
Ta có: Vì OC là phân giác góc xOy nên
AOC = BOC= [tex]\frac{1}{2}[/tex] xOy(1)
theo giả thiết ta có: OA =OB(2)
OC: cạnh chung(3)
Từ (1),(2) và (3) suy ra:AOC=BOC => AC=BC hay C là trung điểm của AB( đpcm)
Bài 2:
GIẢI
a, Ta có : Vì M là trung điểm của AC nên:
AM= MC(1)
theo giả thiết ta lại có: BM= MK(2)
màAMB=KMC( đối đỉnh) (3)
Từ 1, 2,3 suy taAMB=KMC => BAM =KCM = 90
b, Chứng minh tương tự ý a ta có:AMK =BMC => AKM= CBM . Suy ra AK// BC
Bài 3: Cho tam giác ABC, D là trung điểm của AC, E là trung điểm của AB. Trên tia đối của AB. Trên tia đối của tia DB lấy điểm N sao cho DN = DB. Trên tia đối của tia EC, lấy điểm M sao cho EM = EC. Chứng minh rằng A là trung điểm của MN.
P/s: tam giác
: góc
C là trung điểm của AB
GIẢI:
Gọi giao điểm của OC và AB là I
Ta có: Vì OC là phân giác góc xOy nên
AOC = BOC= [tex]\frac{1}{2}[/tex] xOy(1)theo giả thiết ta có: OA =OB(2)
OC: cạnh chung(3)
Từ (1),(2) và (3) suy ra:
AOC=BOC => AC=BC hay C là trung điểm của AB( đpcm)Bài 2:
GIẢI
a, Ta có : Vì M là trung điểm của AC nên:
AM= MC(1)
theo giả thiết ta lại có: BM= MK(2)
mà
AMB=KMC( đối đỉnh) (3)Từ 1, 2,3 suy ta
AMB=KMC => BAM =KCM = 90b, Chứng minh tương tự ý a ta có:
AMK =BMC => AKM= CBM . Suy ra AK// BCBài 3: Cho tam giác ABC, D là trung điểm của AC, E là trung điểm của AB. Trên tia đối của AB. Trên tia đối của tia DB lấy điểm N sao cho DN = DB. Trên tia đối của tia EC, lấy điểm M sao cho EM = EC. Chứng minh rằng A là trung điểm của MN.
P/s
: tam giác: góc
