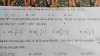Bài này là bài toán đặc trưng dùng đến tâm tỉ cự
Gọi K là điểm thỏa mãn : [tex]\overrightarrow{KA}+2\overrightarrow{KB}+3\overrightarrow{KC}=\overrightarrow{0}[/tex]=>K cố định
Ta có : [tex]MA^2+2MB^2+3MC^2=(\overrightarrow{MK}+\overrightarrow{KA})^2+2(\overrightarrow{MK}+\overrightarrow{KB})^2+3(\overrightarrow{MK}+\overrightarrow{KC})^2=6MK^2+2\overrightarrow{MK}.(\overrightarrow{KA}+2\overrightarrow{KB}+3\overrightarrow{KC})+KA^2+2KB^2+3KC^2=6MK^2+KA^2+2KB^2+3KC^2[/tex]
Do K cố định nên [tex]KA^2+2KB^2+3KC^2[/tex] cố định, vậy tổng đã cho nhỏ nhất khi MK nhỏ nhất, hay MK=0, khi đó M trùng K .
Vậy gọi M(x;y) thì theo công thức cộng vecto của pp tọa độ ta sẽ tìm được x,y thỏa mãn [tex]\overrightarrow{MA}+2\overrightarrow{MB}+3\overrightarrow{MC}=\overrightarrow{0}[/tex]
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
