Anh không biết có cách nào ngắn hơn không nhưng mà cách anh hơi dài =))
Gọi [imath]S[/imath] là giao điểm của [imath]AP[/imath] với [imath](O)[/imath], [imath]M[/imath] là trung điểm [imath]BC[/imath], [imath]SM[/imath] cắt [imath](O)[/imath] tại [imath]D[/imath]. Ta sẽ chứng minh [imath]QH[/imath] chính là đường thẳng Steiner của điểm [imath]D[/imath] với [imath]\Delta ABC[/imath].
Nhận xét 1: [imath]\widehat{ADQ}=90^o[/imath]
Chứng minh:
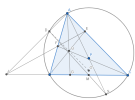
Gọi giao điểm của [imath]BQ[/imath] với [imath]AC[/imath] là [imath]E[/imath], giao điểm của [imath]CQ[/imath] với [imath]AB[/imath] là [imath]F[/imath], giao điểm của [imath]AQ[/imath] với [imath]BC[/imath] là [imath]G[/imath].
Gọi [imath]J[/imath] là giao điểm [imath]EF[/imath] với [imath]BC[/imath], [imath]JA[/imath] cắt [imath](O)[/imath] tại [imath]D'[/imath] khác [imath]A[/imath].
Ta có [imath]\widehat{ABQ}=\widehat{PBC}=\widehat{PCB}=\widehat{ACQ}[/imath] nên [imath]BFEC[/imath] nội tiếp
Khi đó ta thấy [imath](JG,BC)=-1[/imath] nên [imath]JG \cdot JM=JB \cdot JC=JD' \cdot JA=JE \cdot JF[/imath] hay [imath]AD'GM[/imath] nội tiếp.
Mặt khác, [imath]\widehat{GAD}=\widehat{GAB}+\widehat{BAD}=\widehat{PAC}+\widehat{BAD}=\widehat{BAD}+\widehat{SAC}=\widehat{GMD}[/imath] nên [imath]ADGM[/imath] nội tiếp.
Từ đó [imath]D \equiv D'[/imath]. Ta cũng suy ra được [imath]D[/imath] là điểm Miquel của tứ giác toàn phần [imath]BFEC.AJ[/imath]
Gọi [imath]O'[/imath] là tâm của [imath](BFEC)[/imath] thì áp dụng định lý Brocard, ta có [imath]O'Q \perp AJ[/imath] tại [imath]D[/imath], tức [imath]\widehat{ADQ}=90^o[/imath]
Nhận xét 2: [imath]Q[/imath] thuộc đường thẳng Steiner của điểm [imath]D[/imath] ứng với [imath]\Delta ABC[/imath].
Chứng minh:
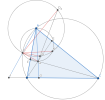
Gọi [imath]D_1,D_2[/imath] lần lượt là điểm đối xứng với [imath]D[/imath] qua [imath]AB,AC[/imath], [imath]K[/imath] là giao điểm của [imath](AQ)[/imath] với [imath](A,AD)[/imath]
Dễ thấy [imath](A,AD)[/imath] đi qua [imath]D_1,D_2[/imath] và [imath]K[/imath] đối xứng với [imath]D[/imath] qua [imath]AQ[/imath]. Từ đó [imath]QD=QK[/imath].
Mà [imath]QD \perp AD[/imath] nên [imath]QD,QK[/imath] là tiếp tuyến của [imath](A,AD)[/imath].
Từ đó ta chỉ cần chứng minh [imath](DK,D_1D_2)=-1 \Leftrightarrow D(QK,D_1D_2)=-1[/imath]
Nhận thấy rằng [imath](JG,BC)=-1 \Rightarrow A(JG,BC)=-1[/imath].
Mà [imath]AJ \perp DQ, AG \perp DK, AB \perp DD_1, AC \perp DD_2[/imath] nên [imath]D(QK,D_1D_2)=-1[/imath].
Nhận xét 3: [imath]T[/imath] thuộc đường thẳng Steiner của [imath]D[/imath] ứng với [imath]\Delta ABC[/imath].
Chứng minh:
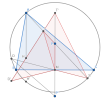
Ta có kết quả quen thuộc là đường thẳng Steiner ứng với [imath]\Delta ABC[/imath] thì đi qua trực tâm [imath]H[/imath] nên nếu gọi [imath]D'[/imath] là điểm đối xứng với [imath]D[/imath] qua [imath]BC[/imath] thì ta chỉ cần chứng minh [imath]T,H,D'[/imath] thẳng hàng là xong.
Giả sử [imath]D'H[/imath] cắt [imath]PS[/imath] và [imath]PM[/imath] tại [imath]I[/imath] và [imath]T'[/imath]. Gọi [imath]H'[/imath] là điểm đối xứng với [imath]H[/imath] qua [imath]BC[/imath] thì [imath]A,H,H'[/imath] thẳng hàng.
Vì [imath]AH \parallel PM[/imath] nên [imath]\widehat{T'PI}=\widehat{H'AS}=\widehat{H'DM}=\widehat{HD'M}=\widehat{ID'M} \Rightarrow ID'MP[/imath] nội tiếp
[imath]\Rightarrow \widehat{D'PM}=\widehat{D'IM}[/imath]
Lại có: [imath]\widehat{MT'I}=\widehat{DHH'}=\widehat{D'H'H}=\widehat{DH'A}=\widehat{MSI} \Rightarrow IT'SM[/imath] nội tiếp
[imath]\Rightarrow \widehat{D'IM}=\widehat{T'SM}[/imath]
Lấy [imath]P'[/imath] đối xứng với [imath]P[/imath] qua [imath]BC[/imath] thì [imath]\widehat{DP'M}=\widehat{D'PM}=\widehat{T'SM} \Rightarrow T'DP'S[/imath] nội tiếp
[imath]\Rightarrow MT' \cdot MP'=MD \cdot MS=MB \cdot MC[/imath]
Mà [imath]T[/imath] là trực tâm [imath]\Delta PBC \Rightarrow MT \cdot MP=MB \cdot MC \Rightarrow MT \cdot MP=MT' \cdot MP'[/imath]
Vì [imath]MP=MP \Rightarrow MT=MT' \Rightarrow T \equiv T' \Rightarrow T,D',H[/imath] thẳng hàng.
Từ [imath]3[/imath] nhận xét trên ta được [imath]T,Q,H[/imath] thẳng hàng.
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé ^^ Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại đây nhé
Bài giảng Trường hè học sinh - giáo viên trường THPT chuyên 2022 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.




