Ta đưa về mô hình theo [imath]\Delta DEF[/imath] như sau:
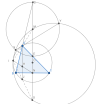
"Cho [imath]\Delta ABC[/imath] nội tiếp [imath](O)[/imath], trung trực của [imath]BC[/imath]cắt [imath]AB,AC[/imath]tại [imath]D,E[/imath]. Tiếp tuyến tại [imath]B,C[/imath]của [imath](O)[/imath]cắt nhau tại [imath]S[/imath]. Đường tròn đường kính [imath]DE[/imath]cắt tiếp tuyến tại [imath]A[/imath]của [imath](O)[/imath]tại [imath]X,Y[/imath]. Chứng minh [imath](SXY)[/imath]tiếp xúc với [imath](O)[/imath]"
Gọi [imath]I[/imath] là giao điểm của [imath](AH)[/imath] với [imath](O)[/imath], [imath]H[/imath] là trực tâm [imath]\Delta ABC[/imath], [imath]J[/imath] là giao điểm [imath]AH[/imath] với [imath](O)[/imath], [imath]M,N[/imath] là trung điểm [imath]DE,BC[/imath] thì ta có một số kết quả quen thuộc:
+ [imath]I,H,N[/imath] thẳng hàng
+ [imath](IJ,BC)=-1[/imath]
Từ đó [imath](IJ,BC)=-1[/imath] ta có [imath]I,J,S[/imath] thẳng hàng.
Lại có [imath]A(IJ,BC)=-1=A(MJ,DE)[/imath] nên [imath]I,A,M[/imath] thẳng hàng.
Dễ thấy [imath]\Delta OAE \sim \Delta ODA \Rightarrow OE \cdot OD^2=OA^2[/imath]
Suy ra [imath](O)[/imath] trực giao với [imath](DE)[/imath]. Từ đó [imath]MA\cdot MI=MX^2 \Rightarrow \Delta MXA \sim \Delta MIX \Rightarrow \widehat{MIX}=\widehat{MXA}=\widehat{MYX}[/imath]
[imath]\Rightarrow MXIY[/imath] nội tiếp.
Từ đó [imath]\widehat{XAI}=\widehat{XMI}+\widehat{MXA}=\widehat{XYI}+\widehat{MYX}=\widehat{MYI}[/imath]
Mà [imath]\widehat{XAI}=\widehat{IJA}=\widehat{ISM} \Rightarrow IMYS[/imath] nội tiếp
Suy ra [imath](SXY)[/imath] đi qua [imath]I[/imath].
Xét phép vị tự [imath]\mathcal{V}[/imath] tâm [imath]I[/imath] tỷ số [imath]k=\dfrac{IJ}{IS}[/imath]. Ta có [imath]\mathcal{V}: I \to I, J \to S, A \to M[/imath] nên [imath]\mathcal{V}: (O) \to (SXY)[/imath]
Vì [imath](O)[/imath] và [imath](SXY)[/imath] cùng đi qua [imath]I[/imath] nên [imath](SXY)[/imath] tiếp xúc [imath](O)[/imath] tại [imath]I[/imath].
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé ^^ Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại đây nhé
[Chuyên đề HSGQG] Định lý LTE, cấp của số nguyên và phương trình nghiệm nguyên chứa lũy thừa
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
