Toán 12 hàm hợp

[minhloveftu]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

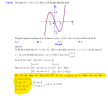
Cho hàm số [imath]y = f(x + 2) - 2022[/imath] có đồ thị như hình vẽ bên dưới
Số giá trị nguyên của tham số [imath]m[/imath] để hàm số [imath]g(x) = f(2x^3 - 6x + m + 1)[/imath] có 6 điểm cực trị

Spoiler: Lời giải

ai giải thích cho em khúc bôi vàng với ạ @Timeless time

 

[Timeless time]

View attachment 208307
ai giải thích cho em khúc bôi vàng với ạ @Timeless time

landghostỞ bước này người ta làm hơi tắt, em vẽ BBT ra cho dễ hình dung nhé
[imath]\begin{array}{c|cccccccc} x & -\infty & & -1 & & 1 & & +\infty \\ \hline h'(x) & & + & 0 & - & 0 & + \\ \hline & & & 4 & & & & & +\infty \\ h(x) & & \nearrow & & \searrow & & & \nearrow & \\ & -\infty & & & & - & 4 & & \end{array}[/imath]

Nhìn vào BBT ta thấy để [imath]g(x)[/imath] có 6 cực trị thì
TH1: (1) có 3 nghiệm lẻ và (2) có 1 nghiệm lẻ
[imath]\implies[/imath] Để (1) có 3 nghiệm lẻ thì [imath]y = -m[/imath] phải cắt [imath]y = h(x)[/imath] tại 3 điểm phân biệt [imath]\implies -4 < - m < 4[/imath]. Để (2) có 1 nghiệm bội lẻ thì [imath]y = 2- m[/imath] phải cắt [imath]y = h(x)[/imath] tại 1 điểm phân biệt [imath]\implies 2 - m \ge 4[/imath]
TH2: (1) có 1 nghiệm lẻ, (2) có 3 nghiệm lẻ
TH này em xét tương tự TH1 nhé

Có gì không hiểu em hỏi lại nha
Xem thêm: [Ôn thi THPTQG] Tài Liệu Ôn Thi THPTQG Môn Toán Lớp 12