- 28 Tháng mười hai 2015
- 229
- 43
- 41
- Bắc Giang
- THPT LG 2
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
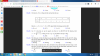 Mọi người hướng dẫn e câu 32 với ạ! Bình thường thì chỉ gặp các bài toán đơn giản thôi, với dạng này thì pp giải như thế nào ạ?
Mọi người hướng dẫn e câu 32 với ạ! Bình thường thì chỉ gặp các bài toán đơn giản thôi, với dạng này thì pp giải như thế nào ạ?
