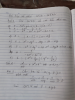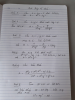Toán 8 GTNN-GTLN

[Tzuyu-chan]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Giúp em với ạ !
@Mộc Nhãn

 

[TranPhuong27]

Bài 3:
[tex]\frac{1}{1+x}+\frac{1}{1+y}+\frac{1}{1+z} \geq 2 \Leftrightarrow \frac{1}{1+x} \geq 1-\frac{1}{1+y}+1-\frac{1}{1+z}=\frac{y}{y+1}+\frac{z}{z+1} \geq 2\sqrt{\frac{yz}{(y+1)(z+1)}}[/tex]
Chứng minh tương tự: [tex]\frac{1}{1+y} \geq 2\sqrt{\frac{zx}{(1+z)(1+x)}};\frac{1}{1+z} \geq 2\sqrt{\frac{xy}{(1+x)(1+y)}}[/tex]
Nhân theo vế 3 BĐT:
[tex]\frac{1}{(x+1)(y+1)(z+1)} \geq 8\frac{xyz}{(x+1)(y+1)(z+1)}[/tex]
[tex]\Leftrightarrow xyz \leq \frac{1}{8}[/tex]
Dấu "=" xảy ra khi [TEX]x=y=z=\frac{1}{2}[/TEX]

 

[7 1 2 5]

1. a) [tex]A=(x^2-4x+5)(x-1)(x-3)=(x^2-4x+5)(x^2-4x+3)=(x^2-4x+4)^2-1=(x-2)^4-1 \geq -1[/tex]
Dấu "=" xảy ra khi x = 2.
b) [tex]3x^2-x+7=3(x^2-\frac{1}{3}x+\frac{7}{3})=3[(x-\frac{1}{6})^2]+\frac{83}{12} \geq \frac{83}{12}[/tex]
Dấu "=" xảy ra khi [tex]x=\frac{1}{6}[/tex]
c) [tex]x^4-2x^3+3x^2-2x+1=(x^2-2x+1)^2=(x-1)^4\geq 0[/tex]
Dấu "=" xảy ra khi x = 1.
d) [tex]|x-5|+|x-10|=|10-x|+|x-5|\geq |10-x+x-5|=5[/tex]
Dấu "=" xảy ra khi [tex](10-x)(x-5) \geq 0 \Leftrightarrow 5 \leq x \leq 10[/tex]
e) [tex]x^2+2y^2-2xy+2x-10y=(x^2+y^2+1-2xy+2x-2y)+(y^2-8y+16)-17=(x-y+1)^2+(y-4)^2-17 \geq -17[/tex]
Dấu "=" xảy ra khi x = 3,y = 4.
f) [tex]x^2+6y^2+14z^2-8yz+6zx-4xy=(x^2+4y^2+9z^2-4xy+6zx-12yz)+(y^2+4yz+4z^2)+y^2+z^2=(x-2y+3z)^2+(y+2z)^2+y^2+z^2 \geq 0[/tex]
Dấu "=" xảy ra khi x = y = z = 0.
h) [tex]\frac{5}{-8x^2+6x-5}=\frac{5}{-2(4x^2-6x+\frac{9}{4})-\frac{1}{2}}=\frac{5}{-\frac{1}{2}-2(2x-\frac{3}{2})^2}=-\frac{5}{\frac{1}{2}+(2-\frac{3}{2})^2} \geq \frac{-5}{\frac{1}{2}}=-10[/tex]
Dấu "=" xảy ra tại [tex]x=\frac{3}{4}[/tex]
k) [tex](x^2+\frac{1}{y^2})(y^2+\frac{1}{x^2})=2+x^2y^2+\frac{1}{x^2y^2}\geq 2+2\sqrt{x^2y^2.\frac{1}{x^2y^2}}=4[/tex]
Dấu "=" xảy ra khi [tex]xy=\pm 1[/tex]
2. [tex]a^2+b^2+\frac{2}{ab}\geq 2ab+\frac{2}{ab}\geq 2\sqrt{2ab.\frac{2}{ab}}=4[/tex]
Dấu "=" xảy ra khi [tex]a=b=1[/tex]

 

[Tzuyu-chan]

@iceghost ,@Mộc Nhãn ,@Lindlar Catalyst

 

[iiarareum]

View attachment 152667
@iceghost ,@Mộc Nhãn ,@Lindlar Catalyst

Bài 5 Theo BĐT Bunyakovsky
[tex](x+3y)^2\leq (1+3)(x^2+3y^{2})=>x^2+3y^{2}\geq \frac{25}{4}[/tex]
Dấu ''='' xảy ra <=> .....
Bài 6
[tex]\frac{x}{x^4+y^2}\leq \frac{x}{2x^{2}y}=\frac{1}{2xy}=\frac{1}{2}[/tex]
CMTT => VT <= 1/2 + 1/2 = 1
Dấu ''='' xảy ra <=>....
Bài 7
[tex]\frac{1}{x^2+y^2}+\frac{1}{2xy}+\frac{1}{4xy}+4xy+\frac{5}{4xy}\geq \frac{4}{(x+y)^{2}}+2+\frac{5}{(x+y)^{2}}\geq 4+2+5=11[/tex]
Dấu ''='' xảy ra <=>....
Bài 3
[tex]\frac{A}{4}=\frac{x^2+y^2}{x^2+y^2-xy}<=>\frac{A}{4}=\frac{\frac{x^2}{y^2}+1}{\frac{x^2}{y^2}-\frac{x}{y}+1}[/tex]
Đặt x/y=a [tex]=> \frac{A}{4}=\frac{a^2+1}{a^2-a+1}<=>A(a^2-a+1)=4(a^2+1)<=>a^{2}(A-4)-aA-(A-4)=0[/tex] (1)
Pt (1) nghiệm <=> [tex]\Delta = A^2-4(A-4)^{2}\geq 0 <=> 3A^{2}-32A+64\leq 0 <=> \frac{8}{3}\leq A\leq 8[/tex]
MinA = 8/3 <=> ....
MaxA=8 <=>......
Bài 4 (Sao mình không thấy câu hỏi nhỉ?)
Bài 8 Áp dụng BĐT [tex]2(a^2+b^2)\geq (a+b)^2 <=> (a-b)^2\geq 0[/tex] luôn đúng
[tex](x+2y)^2\leq 2(x^2+4y^2)=50 => -5\sqrt{2}\leq x+2y\leq 5\sqrt{2}[/tex]
Dấu ''='' xảy ra <=>......

 

[Tzuyu-chan]

Bài 4 (Sao mình không thấy câu hỏi nhỉ?)

Tìm giá trị lớn nhất ạ