View attachment 215453
Câu 1:
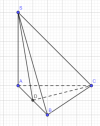
a) [imath]SA\bot (ABC)\Rightarrow SA\bot BC[/imath]
b) Gọi D là trung điểm AB
[imath]\Rightarrow CD\bot AB[/imath]
[imath]CD\bot SA (SA\bot (ABC))[/imath]
Suy ra [imath]CD\bot (SAB)[/imath]
[imath]\Rightarrow (SC,(SAB))=\widehat{CSD}[/imath]
[imath]SC=\sqrt{AC^2+SA^2}=a\sqrt2; CD=\dfrac{a\sqrt3}2[/imath]
[imath]CD\bot (SAB)\Rightarrow CD\bot SD[/imath]
[imath]\sin \widehat{CSD}=\dfrac{CD}{SC}=\dfrac{\sqrt6}4[/imath]
[imath]\Rightarrow (SC,(ABC))=\arcsin\dfrac{\sqrt6}4[/imath]
Có gì khúc mắc em hỏi lại nha
Ngoài ra, em xem thêm tại
Tổng hợp những bài toán HHKG thường gặp
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.