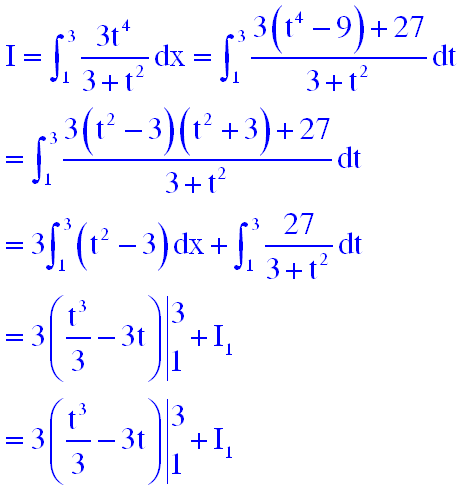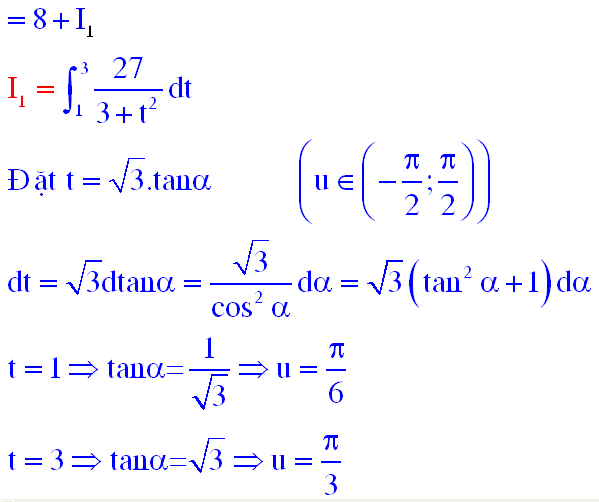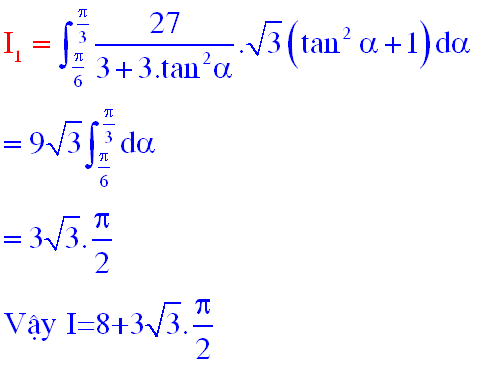giúp mình với !!!!!!!!!!

P

piterpan

alone_9x said:
[TEX]\int_{}^{}\frac{\sqrt[3]{(x-2)^2}}{3+\sqrt[3]{(x-2)^2}}[/TEX]
hix mình ko biết đánh cận nên đành viết riêng ra là cận từ 3 đến 29
mấy bác giúp em với nha !!!
Bấm để xem đầy đủ nội dung ...
đặt u=x-2
du=dx
khi x=3=>u=1
khi x=29=>u=27
[TEX]\int\limits_{1}^{27}\frac{(u^2/3)du}{3+u^2/3}[/TEX]
=1/3[TEX]\int\limits_{1}^{27}\(u^2/3)du[/TEX] + [TEX]\int\limits_{1}^{27}du[/TEX]
=372/5
@-):)>-=((
nếu có gì sai mong các bác chỉ giáo:)|
 
A

alone_9x

piterpan said:
đặt u=x-2
du=dx
khi x=3=>u=1
khi x=29=>u=27
[TEX]\int\limits_{1}^{27}\frac{(u^2/3)du}{3+u^2/3}[/TEX]
=1/3[TEX]\int\limits_{1}^{27}\(u^2/3)du[/TEX] + [TEX]\int\limits_{1}^{27}du[/TEX]
=372/5
@-):)>-=((
nếu có gì sai mong các bác chỉ giáo:)|
Bấm để xem đầy đủ nội dung ...

[TEX]\int\limits_{1}^{27}\frac{(u^2/3)du}{3+u^2/3}[/TEX]
=1/3[TEX]\int\limits_{1}^{27}\(u^2/3)du[/TEX] + [TEX]\int\limits_{1}^{27}du[/TEX ????? bác rút 1/3 ở đâu vậy ??? hình như là had problem rồi :D:D [TEX]\int\limits_{1}^{27}\frac{(u^2/3)du}{3+u^2/3}[/TEX]
[TEX]int\limits_{1}^{27}\frac{du}{1} +\int\limits_{1}^{27}\frac{(3)du}{3+u^(2/3)}[/TEX]
mình làm ra cái thứ 2 thì ko biết làm nên post lên cho mọi người giải hộ :D:D
 
T

teddy_dh1007

hĩ tớ hok bik đánh cái nì!! tớ làm như sau : đến cái chỗ bạn đặt , làm típ như thế nì hok bik đúng hok:
\int_{}^{}(u^2/3 +3 -3)dx/(3+ u^2/3) cận từ 1->27
tách ra thành hai tích phân là \int_{}^{}dx-3\int_{}^{}1dx/(3+u^2/3) xog ùi! ngang đó bạn nguyen hàm thay cận vào là ok . hok bik đúng hok nữa.pà kon cho í kiến nha ;);)
 
X

xalem92

alone_9x said:
[TEX]\int\limits_{1}^{27}\frac{(u^2/3)du}{3+u^2/3}[/TEX]
=1/3[TEX]\int\limits_{1}^{27}\(u^2/3)du[/TEX] + [TEX]\int\limits_{1}^{27}du[/TEX ????? bác rút 1/3 ở đâu vậy ??? hình như là had problem rồi :D:D [TEX]\int\limits_{1}^{27}\frac{(u^2/3)du}{3+u^2/3}[/TEX]
[TEX]int\limits_{1}^{27}\frac{du}{1} +\int\limits_{1}^{27}\frac{(3)du}{3+u^(2/3)}[/TEX]
mình làm ra cái thứ 2 thì ko biết làm nên post lên cho mọi người giải hộ :D:D
Bấm để xem đầy đủ nội dung ...

Tính[TEX]I_2=\int\limits_{1}^{27}\frac{du}{\sqrt[3]{u^2}+3}[/TEX]

đặt [TEX]\sqrt[3]{u}=\sqrt{3}tant[/TEX]

\Rightarrow[TEX]\frac{dx}{3\sqrt[3]{u^2}}=\sqrt{3}(tan^2x+1)dt[/TEX]

u=1\Rightarrowt=[TEX]\frac{\pi}{6}[/TEX]
u=27\Rightarrowt=[TEX]\frac{\pi}{3}[/TEX]
...........
[TEX]I_2=3\sqrt{3}\int\limits_{\frac{\pi}{6}}^{\frac{\pi}{3}}tan^2tdt[/TEX]

\RightarrowKquả [TEX]I_2=6-\frac{\sqrt{3}\pi}{2}[/TEX]

Vậy [TEX]I=\frac{3\sqrt{3}\pi}{2}+8[/TEX]
(mình thử lại = máy tính rùi)
 
A

alone_9x

hix thì ra là công thức đặt x = atant
thak bạn
ah mà bạn bấm máy tính như thế nào ra tích phân hay vậy chỉ mình với ...
 
K

kimduong92

tính tích phân chỉ có ở 570ES thôi cậu ạh nếu có thi` cái phím kia ở ngay dưới phím alpha đó cậu nhập các gt vào ui` = là dc :D
 
K

kaitomovei

các em cố lên. thực chất mấy bài tích phân không khó lắm đâu. các em chịu khó suy nghĩ tý là đc liền ah, nhưng các em phải cố gắng nhận dạng của nó nhé. Chúc các em học tốt
 
K

kaitomovei

các em thử tính bài này xem nhé tích phân đi từ 2009 ->2010 của căn bậc 2 của (x^2+1) dx
 
X

xalem92

máy tính 570ES hoặc MS cũng tính đc TP. tính tích phân xong thì thử tính lại bằng máy tính cho chắc ăn
 
A

alone_9x

************************************************************************************************************************************************************************************************aaaaaaaa
gửi nhầm địa chỉ :((
 
Last edited by a moderator:
A

alone_9x

kaitomovei said:
các em thử tính bài này xem nhé tích phân đi từ 2009 ->2010 của căn bậc 2 của (x^2+1) dx
Bấm để xem đầy đủ nội dung ...


ặc ặc bài khó quá ...
hình như cái này là tích phân từng phần
giải thử hên xui :D:D

I = [TEX]\int\limits_{2009}^{2010}\sqrt[]{x^2 + 1}[/TEX]
đặt u =[TEX]\sqrt[]{x^2 + 1} ==> du = \frac{x}{\sqrt[]{x^2 + 1}}[/TEX]
.......dv= dx ===========> v =x
=>I = [TEX]x{\sqrt[]{x^2 + 1}}|? - \int\limits_{2009}^{2010}\frac{x^2}{\sqrt[2]{x^2 + 1}}[/TEX]
tính tiếp cái tích phân kia rra :D
hình như là J =[TEX]\int\limits_{2009}^{2010}\frac{(x^2 +1) - 1}{\sqrt[]{x^2 + 1}}[/TEX]
tách tích phân ta được 1 cái là I như ban đầu còn cái kia thì phải đặt(gọi là K )
t=[TEX]ln(x+{\sqrt[]{x^2 + 1}}[/TEX]
dt=[TEX]\frac{dx}{\sqrt[]{x^2 + 1}}[/TEX]
đổi cận
x...2009................2010
t ...(ai đổi hộ mình đi nhỉ @-) b-( )
=> K = [TEX]\int_{}^{}dt = t |?[/TEX]
thay vào ban đầu thì I =[TEX]x{\sqrt[]{x^2 + 1}}|? - I + K (J = I -K)[/TEX]
..................................mọi người giúp e thay cận nhé e bùn ngủ qué rùi @-)@-)@-)@-)
..................................nhìn là CHOÁNG................................
hok biết đúng hok nữa sao thấy choáng quá :((
thay số và thay cận là cả 1 vấn đề ...
 
Last edited by a moderator:
A

alone_9x

....................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
....................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
 
Last edited by a moderator:
D

dhg22adsl

alone_9x said:
[TEX]\int\limits_{3}^{29}\frac{\sqrt[3]{(x-2)^2}dx}{3+\sqrt[3]{(x-2)^2}}[/TEX]
mấy bác giúp em với nha !!!
Bấm để xem đầy đủ nội dung ...
1-33.png

2-28.png

3-13.png

4-7.png
 
A

alone_9x

ai giúp mình làm bài này nha :)

[TEX]\int\limits_{0}^{pi}sin^{n-1} x * cos(n+1)x dx[/TEX]
 
Last edited by a moderator:
C

cuongbrvt

hay wa ha dzay tinh gium cai bai nay di ban
\int_{}^{} (cosx^n)(cos(n+2)xdx giai ho minh dc hok cac ban:-SS
 
You must log in or register to reply here.
Top Bottom