T
trangbu99
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
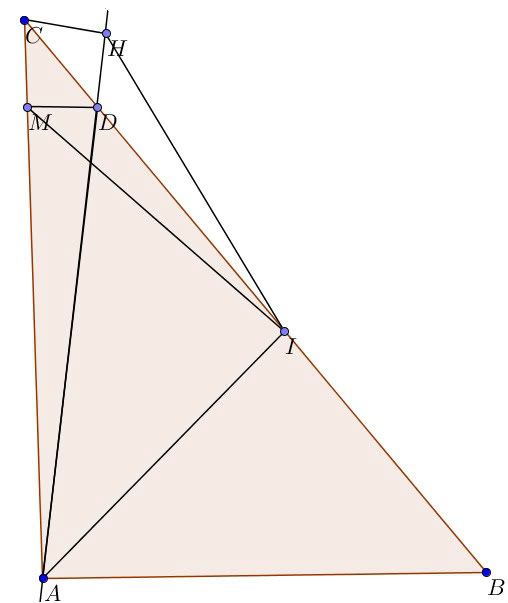
Cho tam giác ABC có góc A vuông và AB<AC.Kẻ AI vuông góc BC. Trên BC lấy D sao cho BI=ID.CMR
a)tam giác ABI= tam giác ADI.
b)kẻ CH vuông góc AD. CMR CD là fg goc ACH.
c)kẻ DM vuông góc AC. CMR IH=IM=IA


Thank trước nhé:-j> <;
<;
a)tam giác ABI= tam giác ADI.
b)kẻ CH vuông góc AD. CMR CD là fg goc ACH.
c)kẻ DM vuông góc AC. CMR IH=IM=IA
Thank trước nhé:-j>