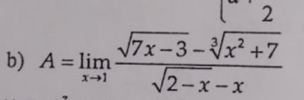[imath]A=\lim_{x\to1} \dfrac{\sqrt{7x-3}-\sqrt[3]{x^2+7}}{\sqrt{2-x}-x}\\=\lim_{x\to1} \left(\dfrac{\sqrt{7x-3}-2}{\sqrt{2-x}-x}+\dfrac{2-\sqrt[3]{x^2+7}}{\sqrt{2-x}-x}\right)\\=\lim_{x\to1} \left(\dfrac{\left(\sqrt{7x-3}-2\right)\left(\sqrt{7x-3}+2\right)\left(\sqrt{2-x}+x\right)}{\left(\sqrt{2-x}-x\right)\left(\sqrt{2-x}+x\right)\left(\sqrt{7x-3}+2\right)}+\dfrac{\left(2-\sqrt[3]{x^2+7}\right)\left(\sqrt[3]{x^2+7}^2+2\sqrt[3]{x^2+7}+4\right)\left(\sqrt{2-x}+x\right)}{\left(\sqrt{2-x}-x\right)\left(\sqrt{2-x}+x\right)\left(\sqrt[3]{x^2+7}^2+2\sqrt[3]{x^2+7}+4\right)}\right)\\=\lim_{x\to1} \left(\dfrac{7\left(x-1\right)\left(\sqrt{2-x}+x\right)}{\left(x-1\right)\left(-2-x\right)\left(\sqrt{7x-3}+2\right)}+\dfrac{\left(x-1\right)\left(-1-x\right)\left(\sqrt{2-x}+x\right)}{\left(x-1\right)\left(-2-x\right)\left(\sqrt[3]{x^2+7}^2+2\sqrt[3]{x^2+7}+4\right)}\right)\\=\lim_{x\to1} \left(\dfrac{7\left(\sqrt{2-x}+x\right)}{\left(-2-x\right)\left(\sqrt{7x-3}+2\right)}+\dfrac{\left(-1-x\right)\left(\sqrt{2-x}+x\right)}{\left(-2-x\right)\left(\sqrt[3]{x^2+7}^2+2\sqrt[3]{x^2+7}+4\right)}\right)[/imath]
Rồi thay [imath]x=1[/imath] vào
Nếu có thắc mắc gì bạn cứ hỏi tại đây, tụi mình sẽ hỗ trợ.
Ngoài ra, bạn tham khảo kiến thức tại topic này nha
https://diendan.hocmai.vn/threads/t...c-mon-danh-cho-ban-hoan-toan-mien-phi.827998/
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.