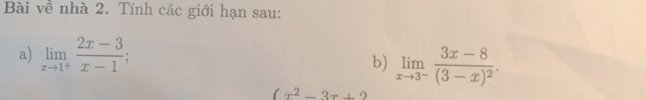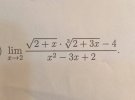1. [imath]\displaystyle \lim _{x \to 1^+} \dfrac{2x-3}{x-1}=\displaystyle \lim _{x \to 1^+} (2-\dfrac{1}{x-1})=2- \displaystyle \lim _{x \to 1^+} \dfrac{1}{x-1}=-\infty[/imath]
2. Đặt [imath]x-3=t[/imath]. Ta có [imath]\displaystyle \lim _{x \to 3^-} \dfrac{3x-8}{(3-x)^2}=\displaystyle \lim _{t \to 0^-} \dfrac{3t+1}{t^2}=+\infty[/imath]
3. Biển đổi [imath]\dfrac{\sqrt{2+x} \cdot \sqrt[3]{2+3x}-4}{x^2-3x+2}=\dfrac{\sqrt{2+x} \cdot \sqrt[3]{2+3x}-2\sqrt{2+x}+2\sqrt{2+x}-4}{x^2-3x+2}[/imath]
[imath]=\dfrac{\sqrt{x+2} \cdot \dfrac{3(x-2)}{\sqrt[3]{(2+3x)^2}+2\sqrt[3]{2+3x}+4}+\dfrac{2(x-2)}{\sqrt{2+x}+2}}{(x-1)(x-2)}[/imath]
[imath]=\dfrac{\dfrac{3\sqrt{x+2}}{\sqrt[3]{(3x+2)^2}+2\sqrt[3]{3x+2}+4}+\dfrac{2}{\sqrt{2+x}+2}}{x-1}[/imath]
[imath]\displaystyle \lim _{x \to 2} \dfrac{\sqrt{2+x} \cdot \sqrt[3]{2+3x}-4}{x^2-3x+2}=\displaystyle \lim _{x \to 2} \dfrac{\dfrac{3\sqrt{x+2}}{\sqrt[3]{(3x+2)^2}+2\sqrt[3]{3x+2}+4}+\dfrac{2}{\sqrt{2+x}+2}}{x-1}=1[/imath]
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé ^^ Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại đây nhé
Giới hạn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
