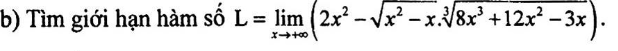Toán 11 giới hạn hàm số

[ln8941595@gmail.com]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Tính giới hạn hàm số [imath]L=\lim _{x \to +\infty} (2x^2-\sqrt{x^2-x}.\sqrt[3]{8x^3+12x^2-3x})[/imath]
Mọi người giúp em với ạ. tiện thể mọi người cho e hỏi ai có đáp án của đề chọn hsg toán 10-11 tỉnh hà tĩnh 2021-2022 không ạ?

 

[7 1 2 5]

Ta có: [imath]2x^2-\sqrt{x^2-x}.\sqrt[3]{8x^3+12x^2-3x}[/imath]
[imath]=\dfrac{1}{2}+\dfrac{1}{2}[4x^2-1-2\sqrt{x^2-x}(2x+1)]+\sqrt{x^2-x}(2x+1-\sqrt[3]{8x^3+12x^2-3x})[/imath]
[imath]=\dfrac{1}{2}+\dfrac{2x+1}{2}.\dfrac{1}{2x-1+2\sqrt{x^2-x}}+\sqrt{x^2-x}.\dfrac{9x+1}{(2x+1)^2+(2x+1)\sqrt[3]{8x^3+12x^2-3x}+\sqrt[3]{(8x^3+12x^2-3x)^2}}[/imath]
[imath]=\dfrac{1}{2}+\dfrac{2+\dfrac{1}{x}}{2}.\dfrac{1}{2-\dfrac{1}{x}+2\sqrt{1-\dfrac{1}{x}}}+\sqrt{1-\dfrac{1}{x}}.\dfrac{9+\dfrac{1}{x}}{(2+\dfrac{1}{x})^2+(2+\dfrac{1}{x})\sqrt[3]{8+\dfrac{12}{x}-\dfrac{3}{x^2}}+\sqrt[3]{(8+\dfrac{12}{x}-\dfrac{3}{x^2})^2}}[/imath]
[imath]\Rightarrow L=\dfrac{1}{2}+\dfrac{2}{2}.\dfrac{1}{2+2}+1.\dfrac{9}{2^2.3}[/imath]
[imath]=\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}=\dfrac{3}{2}[/imath]

Còn đáp án thì mình có đính kèm rồi nhé.

Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé. Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại topic này nha
Giới hạn hàm số