ui trời, sao kô làm cái này sớm tí anh. hix. post bài mà chả ai vào ngó cho, em đưa lên đây nhờ anh xử lí cái.
Cho (Cm) : y=-x^3 + mx^2 -m. và (Dk): y=kx +k+1.
I/ cho m=3.
1)k/s và vẽ đồ thị hs.
2)gọi A và B là 2 điểm CĐ và CT của (C).M là điểm bất kì cung AB của (C).CMR trên (C) ta tìm được 2 điểm tại đó tiếp tuýen vuông góc với tiếp tuyến tại M của (C).
3) gọi (d): y=1. Biện luận số tiếp tuyến với (C) vẽ từ E thuộc (d).
4) tìm điểm E thuộc (d) để qua E kẻ được 3 tiếp tuyến với (C) trong đó có 2 tiếp tuyến vuông góc với nhau.
5) xác định p để trên (C) có 2 tiếp tuyến có hsg =p. Trong TH này, chứng tỏ trung điểm 2 tiếp tuyến là cố định.
6) tìm điểm M trên (C) để qua M chỉ có 1 tiếp tuyến với (C).
II/ cho m thay đổi.
7) C/m (Cm) có 2 điểm cố định. Xác định m để 2 tiếp tuyến tại 2 điểm cố định này vuông góc với nhau.
8) xác định m để (Cm) có 2 điẻm cực trị, viết pt đườn thẳng đi qua 2 điẻm cực trị.
9) xác định m để (Cm) cắt Ox tại 3 điểm pb . với m=? thì (Cm) cắt Ox tại 3 điểm pb với 1 điểm có hoành độ âm, 2 điểm có hoành độ dương.
10) xác định m để h/s ĐB trong khoabngr (1;2)
xác định m để h/s NB trong khoảng (0; cộng vô cùng)
11) tìm đk giữa k và m để (Dk) cắt (Cm) tại 3 điểm pb. tìm k để (Dk) cắt (Cm) thành 2 đoạn bằng nhau.
12) CMR trong các tiếp tuyến với (Cm) thì tiếp tuyến tại điểm uốn có k max. viết pt tiếp tuyến với (Cm) qua A (-1;1).
em cũng làm được nhiều câu nhưng cũng có mấy câu chưa làm được thôi cho cả lên mọi người xem với. bài dài nên nếu ko làm được cụ thể nhờ anh chỉ cho em hướng làm bài ra với.
mọi người giúp mình nhanh với nha, sắp nộp bài rồi!! thank!
Anh hơi bận nên không có thời gian giải chi tiết. Nói chung là những bài toán này e cần chú ý những điểm sau.
1. Điểm thuộc Ox sẽ có dạng A(a, 0), còn thuộc Oy sẽ có dạng (0,b).
2. Phương trình tiếp tuyến có dạng [TEX]y = f'(x_0)(x-x_0) + f(x_0)[/TEX]. Với [TEX]x_0[/TEX] là hoành độ tiếp điểm. Nếu ta chưa biết thì phải giả sử [TEX]M (x_0, f(x_0))[/TEX] là tiếp điểm. Khi đó bao nhiêu [TEX]x_0[/TEX] sẽ có bấy nhiêu tiếp tuyến.
3. Biện luận số tiếp tuyến chính là biện luận số nghiệm [TEX]x_0[/TEX]. Ví dụ câu
3) gọi (d):y=1. Biện luận số tiếp tuyến với (C) vẽ từ E thuộc (d).
- Bước 1: Giả sử tiếp diểm là [TEX]M(x_0, f(x_0))[/TEX]. Suy ra PTTT theo [TEX]x_0[/TEX].
- Bước 2: E thuộc d: y=1 nên E (e,1). TT qua E nên tạo độ của E phải thỏa mãn PTTT. Thế vào PTTT, ta được 1 pt chỉ theo [TEX]x_0[/TEX] (còn e là tham số).
- Bước 3: Số tiếp tuyến được lập chính là số nghiệm [TEX]x_0[/TEX] của PT trên. Vì vậy bài toán chính là biện luận số nghiệm của PT theo e.
Thông thường có hai cách biện luận số nghiệm của PT: thứ nhất là dùng đồ thị (biện luận số giao điểm), thứ hai là dùng tam thức bậc 2.
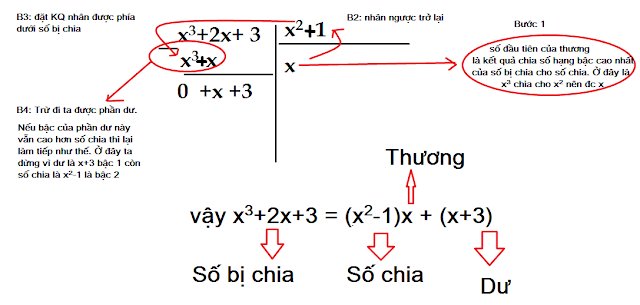
4. Đối với những hàm bậc 3 liên quan đến cực trị nên dùng pp chia y cho y' để tìm PT đường thẳng qua 2 điểm cực trị để bài toán bớt cồng kềnh vì muốn tính y tại cực trị thì thay vào PT dường thẳng sẽ dễ hơn vì là bậc 1, còn thay vào hàm sẽ vất vả hơn vì bậc 3. Đối với hàm phân thức (bậc 2 trên bậc 1)[TEX]\frac{P(x)}{Q(x)}[/TEX] thì công tác tìm PT đường thẳng qua 23 điểm cực trị làm bằng cách lấy dạo hàm tử chia đạo hàm mẫu.
5. Những bài toán như câu 12)
12) CMR trong các tiếp tuyến với (Cm) thì tiếp tuyến tại điểm uốn có k max.
PP làm như sau:
- B1: lấy y' = ....
- B2: giả sử [TEX]x_0[/TEX] là hoành độ tiếp điểm -> hệ số góc [TEX]k = y'(x_0)[/TEX]. khi đó coi k là một hàm theo [TEX]x_0[/TEX]
- B3: khảo sát sơ sơ hàm k, vẽ bảng BB và nhận thấy nó đạt cực đại khi [TEX]x_0[/TEX] bằng hoành độ tại điểm uốn. Vây -> đpcm.
6. Với những bài toán chứng minh đồ thị hàm số luôn đi qua một điểm cố định thông thường ta làm dựa theo nhận xét sau: khi m thay đổi thì đồ thị thay đổi nhưng luôn qua điểm cố định M(a, b) nào đó. Do đó, tọa độ M (a, b) luôn thỏa mãn PT hàm số
với mọi m. Ta chỉ cần thay một vài giá trị dễ tính của m như m = 0, 1, ... vào rồi giải ra a, b.
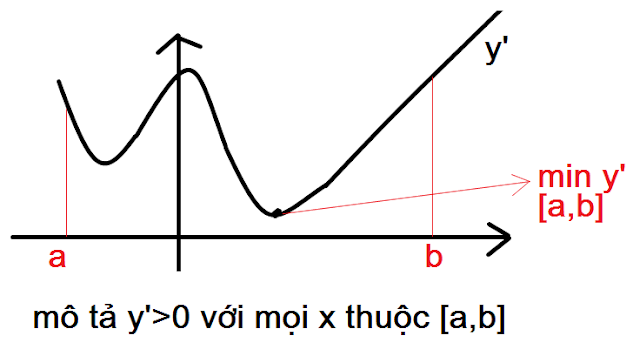
7. Những bài toán yêu cầu tìm m để hs đồng biến (hoặc nghịch biến) trên một miền (a, b) nào đó ta phải tìm m cho y'>=0 với mọi x trên miền đó. Nhận thấy y' > 0 với mọi x thuộc (a,b) -> phần thấp nhất của đồ thị của y' cũng phải nằm trên trục hoành (vì trục hoành là y=0) với mọi x thuộc (a,b). hay min y' trên (a,b) >0. Cái này em có thể vẽ BBT rồ kết luận. Hình vẽ mô tả ở dưới
Còn nhiều dạng toán khác nữa về chuyên đề KSHS lắm. Em cứ làm nhiều là quen thôi. Những dạng toán này về cơ bản không đánh đố và có dạng rõ ràng nên không khó lắm. Chúc em học tốt.

>-
From Rocky