Phương pháp cực trị trong hình phẳng
Hôm nay mình muốn giới thiệu với các bạn lớp 11 một phương pháp giải quyết một số vấn đề về cực trị
hình học phẳng thông qua phép dời hình. Mình đang dạy hai đứa nhóc lớp 11, chúng bảo ở trên lớp bây giờ mới chỉ học đến phép đối xứng trục, và thông thường là một bài trong SGK phải học hơn một tuần mới xong … hic. Mình nghĩ phương pháp học dạng này tốt nhất là học qua lý thuyết càng nhanh càng tốt, để có một cái nhìn tổng quát, rằng chúng ta có khoảng 5 công cụ dời hình, và 5 công cụ này rất đơn giản nhưng ứng dụng nó lại là cả một nghệ thuật

)

)

) Và vì thế, tất lẽ dĩ ngẫu, chúng ta sẽ là những nghệ sỹ =))=))=)) Sau đó là làm bài tập cho từng dạng, rồi nâng cao hơn là những bài cần phối hợp 2 hay nhiều phép dời hình. Mọi lý thuyết sẽ sáng tỏ khi ta làm thành thạo các bài tập (thông thường cần làm n bài cho một dạng với
n →∞ b-( ). Hình học là tư duy trực quan, vì vậy không một lý thuyết nào giúp ta thấu hiểu bản chất của nó bằng các
bài tập và những
hình vẽ. Đó cũng là cách mình truyền tải lý thuyết của phần này:
bài tập và hình vẽ. Bây giờ không dông dài nữa, chúng ta bắt đầu
“cuộc đời của một nghệ sỹ”… =)) =)) =))
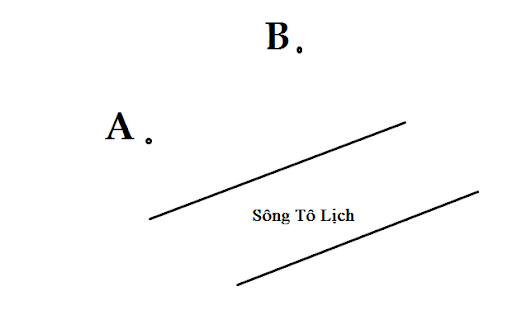
Bài 1: Ở một thành phố nhỏ ven sông đang giải phóng mặt bằng để chuẩn bị quy hoạch một dự án đô thị mới. Các gia đình đều phải giải tỏa và đã chuyển đi nơi khác sau khi nhận một cục tiền đền bù. Tuy nhiên còn ngôi nhà vẫn chưa chịu di dời, đó là nhà của 2 lão Mathematican độc thân (A và B). Vị trí nhà 2 lão như hình vẽ.
Lão chủ thầu khuyên nhủ thế nào cũng không chịu đi (thông thường những nhà toán học thường hay hấp dở kiểu như thế). Lão ta nghĩ ra một cách là cho người phóng hỏa nhà lão B. Và hắn làm thật. Đang giữa trưa, nhà lão B tự dưng cháy, lão vội gọi điện cho ông bạn thân A nhờ chữa cháy giúp, vì tối qua đi tán gái, không biết là chó nhà nàng mới đẻ, hậu quả là bị nó cắn vào chân nên không thể đi lại được

Lão B thấy vậy, không ngại ngần vác một cái thùng phi tức tốc chạy ra bờ sông múc nước cứu bạn. Tuy nhiên toán học đã ngấm vào máu của lão nên chỉ trong [TEX]\frac{1}{1000}[/TEX] giây, lão già A đã tìm ra được đường đi ngắn nhất từ nhà mình đến bờ sông để múc nước, và từ bờ sông đến nhà bạn. Nếu bạn rơi vào trường hợp như vậy bạn sẽ làm thế nào?
Lời giải:
Ta đưa bài toán về dạng như sau:
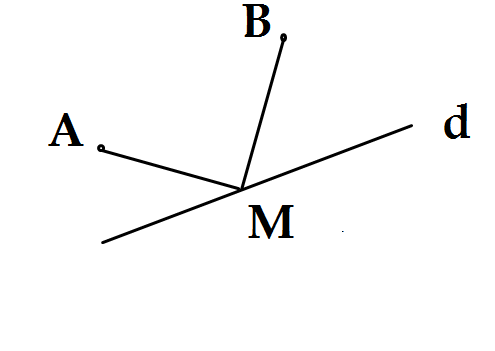
Tìm điểm M (điểm múc nước) thuộc đường thẳng d (bờ sông) sao cho tổng khoảng cách MA + MB là nhỏ nhất (1). Khi ta chưa biết một điều gì thì sự
“tưởng bở” và
“mơ hão” hóa ra lại có vai trò quan trọng

)
Giá mà tìm được điểm M. Vậy ta giả sử đã tìm được M thỏa mãn (1) như hình vẽ.
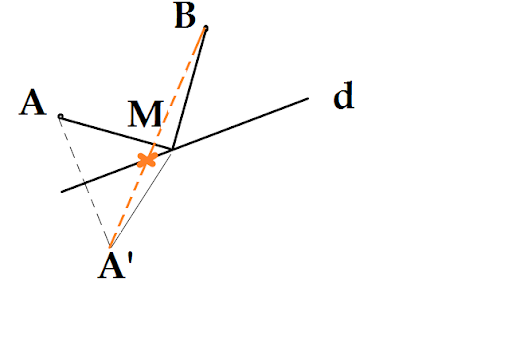
Lấy A’ đối xứng với A qua d, ta sẽ có AM = A’M. Vậy bài toán trở thành:
Tìm M để MA’ + MB là min. Mà ta nhận thấy đoạn nói A’, M, B là một
đường gấp khúc. MA’+MB min khi đường gấp khúc này tiến về một đường thẳng.
Vậy M sẽ là giao của A’B với d. Hình vẽ
Như vậy
ý tưởng sẽ là:
Bài toán yêu cầu tìm min của một tổng S là tổng của hữu hạn các đoạn thẳng. Ta phải dùng những phép dời hình thích hợp để thay thế những đoạn cần thiết bởi những đoạn tương đương. Sao cho tổng cần tính của ta trở thành một đường gấp khúc. Đường này sẽ min khi nó là một đường thẳng. Từ đó rút ra hướng dựng. Cái “giá mà” đã trở thành hiện thực.
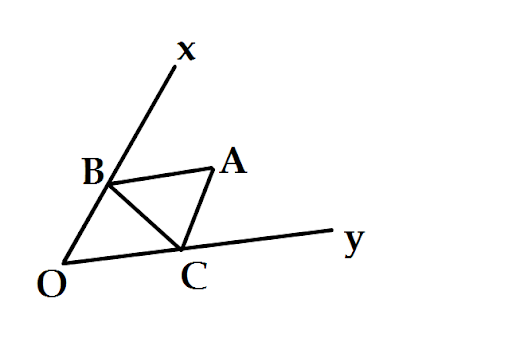
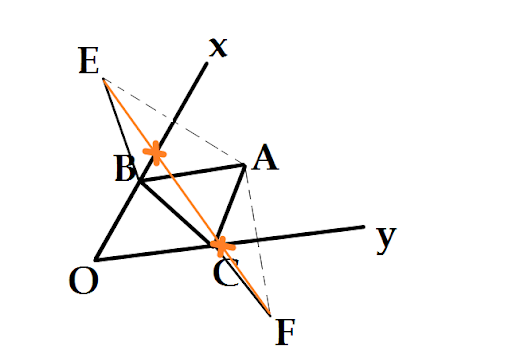
Bài 2: Bây giờ có một góc nhọn xOy và một điểm A bên trong góc này. Hãy tìm B thuộc Ox và C thuộc Oy sao cho chu vi tam giác ABC là min.
Lời giải: Lại là “giá mà tìm được B, C thỏa mãn” thì tốt biết mấy. Khi đó
S = AB + BC + AC min.
Lấy đối xứng của A lần tượt qua Ox, Oy ta được tương ứng E, F . Khi đó AB = EB, AC = FC. Tổng S = EB + BC + CF. Lại là một đường gấp khúc. Tất lẽ dĩ ngẫu, B và C phải là giao của , F với Ox và Oy rồi.
Hai ví dụ trên chúng ta đều sử dụng tính chất của
phép đối xứng trục để giải quyết bài toán dựa trên định hướng
“đưa đường gấp khúc về đường thẳng”
Bài 3: Bây giờ ví dụ cuối cùng. Có 3 thành phố A, B, C nằm ở 3 đỉnh của một tam giác nhọn. Tất cả người dân trong thành phố đều có sở thích ăn gà rán
KFC. Tuy nhiên KFC dạo này đang làm ăn thua lỗ nên không thể đầu tư xây tại mỗi thành phố một nhà hàng được. Vì vậy , học quyết định xây một nhà hàng ở trong lòng tam giác, sao cho tổng khoảng cách từ nhà hàng đến trung tâm 3 thành phố là ngắn nhất. Nếu KFC thuê bạn thiết kế, bạn sẽ làm ntn?
Lời giải: Lại
“giá mà” nhé

) ta sẽ có hình vẽ
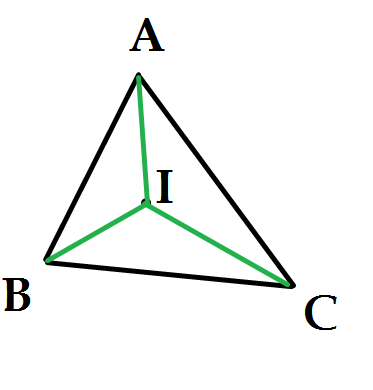
Bài toán trở thành:
Tìm điểm I bên trong tam giác nhọn ABC, sao cho S = IA + IB + IC là min.
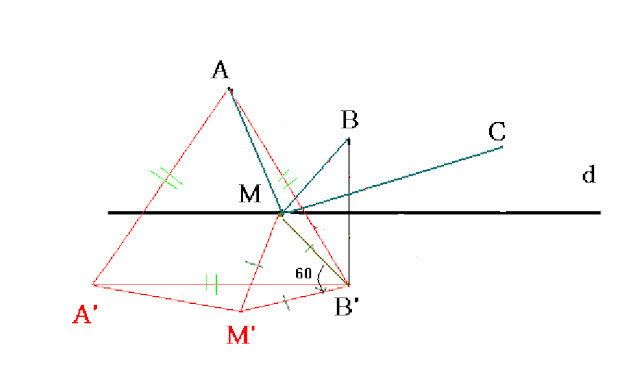
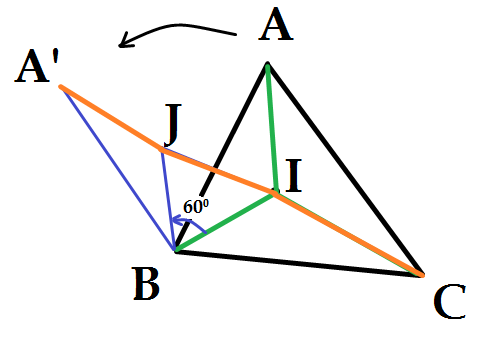
Thực hiện phép quay tâm B, với góc quay 60 độ biến I thành J và biến A thành A’. Khi đó tam giác BIJ đều, vì BI =BJ và B = 60 độ → BI = IJ. Mặt khác, AI = A’J do phép quay là một phép dời hình biến một đoạn thành một đoạn bằng nó.
Ta có
Vậy
S = A’J + JI + IC. Lại là một
đường gấp khúc. Để S min thì I, J phải nằm trên đường thẳng A’C sao cho BIJ là tam giác đều. Vậy cách dựng như sau
- Bước 1: Dựng A’ là ảnh của A qua phép quay tâm B một góc 60 độ
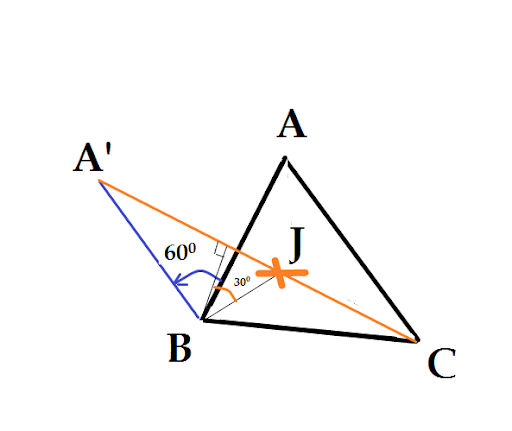
- Bước 2: Kẻ BH vuông góc A’C. Sau đó lấy I trên A’C sao cho BHI = 30 độ.
Vậy I là điểm cần tìm
Trên đây là 3 ví dụ Rocky đưa ra để các bạn nắm được
tư tưởng chung về hướng giải quyết một bài toán liên quan đến
vấn đề cực trị trong hình học phẳng. Có thể tóm tắt lại là:
Bước 1: Xây dựng mô hình toán học cho bài toán. Tức là biến bài toán thực tế về ngôn ngữ toán học. Ví dụ trong bài 3 ta biến 3 thành phố A, B, C thành 3 đỉnh của 1 tam giác; quán gà rán KFC là điểm I …
Bước 2: Giả sử bài toán đã giải xong. Từ đó ta tìm ra những tính chất đặc biệt, rồi suy ngược lại cách dựng.
Thông thường ta phải biến tổng S thành tổng của các đoạn thẳng, mà các đoạn này lập thành một đường gấp khúc. S min khi đường gấp khúc là một đường thẳng.
Hy vọng sẽ có ích cho các bạn.

>-
From Rocky
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
 Vì vậy mọi người post toán lên pic này nhé. Post lên pic kia mod mà nhìn thấy sẽ "làm thịt" cả mình lẫn các bạn đấy
Vì vậy mọi người post toán lên pic này nhé. Post lên pic kia mod mà nhìn thấy sẽ "làm thịt" cả mình lẫn các bạn đấy  )
)  )
)  )
) >-
>-