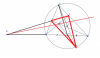
Qua A kẻ đường thẳng vuông góc với DH, cắt BC tại N.
Gọi I là giao điểm của KH và AN
Ta có tứ giác BFEC; AFHI nội tiếp nên [tex]\widehat{FAH}=\widehat{FIH}[/tex]
Mà [tex]\widehat{FAH}=\widehat{FCB}\Rightarrow \widehat{FIH}=\widehat{FCB}[/tex] (1)
ta có: tứ giác AFHE nội tiếp nên năm điểm A, F, H, I, E nội tiếp
Có: [tex]DB.DC=DF.DE=DH.DI[/tex] -> BHIC là tgnt [tex]\Rightarrow \widehat{HIB}=\widehat{HCB}[/tex] (2)
(1,2) -> [tex]\widehat{FID}=\widehat{HIB} \Rightarrow \widehat{AIF}=\widehat{BIN}[/tex]
Lại có [tex]\widehat{ACB}=\widehat{AFE}=\widehat{AIE}\Rightarrow IECN[/tex] là tgnt [tex]\Rightarrow AI.AN=AE.AC[/tex]
Mà [tex]AF.AB=AE.AC \Rightarrow AF.AB=AI.AN\Rightarrow FINB[/tex] là tgnt
[tex]\Rightarrow \widehat{BFN}=\widehat{BIN}=\widehat{AIF}=\widehat{FBN}\Rightarrow \widehat{NFC}=\widehat{NCF}[/tex]
-> CNF cân tại N -> FN=CN. Mà tam BFC vuông tại F -> FN=CN=NB -> N là trung điểm BC -> N trùng M -> đpcm
Mình không biết làm như này được không nhỉ. Mình nghĩ được như này vì trước mình đã làm 1 bài tương tự, chỉ đảo lại gt và kl của bài này thôi ^^