Toán Đường tròn

[Uchiha Sasuke']

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

 

[iceghost]

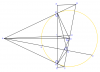
d) Từ $B, C$ kẻ các đường thẳng song song $IH$ cắt $MN$ lần lượt tại $P$ và $Q$
Do $\widehat{IMO} = \widehat{OAB}$ (cùng phụ $\widehat{MOA}$ và $\widehat{IOM} = \widehat{OBA}$ (cùng phụ $\widehat{MOB}$ nên $\triangle{MIO} \sim \triangle{AOB}$ (g-g), suy ra $\dfrac{IM}{OA} = \dfrac{MO}{AB}$ hay $IM \cdot AB = OA \cdot MO$
Tương tự ta cũng có $IN \cdot AC = OA \cdot NO$, suy ra $IM \cdot AB = IN \cdot AC ( = OA \cdot R )$
Theo định lý Ta-lét ta lại có $\dfrac{IP}{IM} = \dfrac{AB}{AM} \iff IP \cdot AM = IM \cdot AB$ và $\dfrac{IQ}{IN} = \dfrac{AC}{AN} \iff IQ \cdot AN = IN \cdot AC$
Suy ra $IP \cdot AM = IQ \cdot AN$ hay $IP = IQ$ do $AM = AN$ theo tính chất hai tiếp tuyến cắt nhau. Từ đó theo tính chất đường trung bình trong hình thang ta có $HB = HC$ hay $H$ là trung điểm $BC$