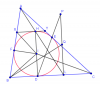
5) Câu a kinh điển quá rồi, mình xin giới thiệu 1 cách:
a) Kẻ đường kính $DH'$. Gọi $L'$ là giao của $AH'$ với $BC$. Ta chứng minh $L'$ trùng $L$
Qua $H'$ kẻ tiếp tuyến $XY$ của $(I)$
Do $IX$ và $IB$ là hai tia phân giác của hai góc kề bù $H'IF$ và $DIF$ nên $IX$ vuông góc $IB$
Từ đó có $FX \cdot FB = FI^2$. Tương tự thì $EY \cdot EC = EI^2 = FX \cdot FB$
Theo tính chất hai tiếp tuyến cắt nhau thì $EY = H'Y$, $EC = DC$, $FX = H'X$ và $FB = DB$
Do đó $H'Y \cdot DC = H'X \cdot DB \ (1)$
Lại theo định lý Ta-lét thì $\dfrac{H'X}{L'B} = \dfrac{AH'}{AL'} = \dfrac{H'Y}{L'C}$
Suy ra $H'Y \cdot L'B = H'X \cdot L'C \ (2)$
Chia vế theo vế hai đẳng thức $(1)$ và $(2)$ ta thu được $\dfrac{DC}{L'B} = \dfrac{DB}{L'C} = \dfrac{DC + DB}{L'B + L'C} = 1$
Suy ra $DC = L'B$ và $DB = L'C$, suy ra $D$ và $L'$ đối xứng nhau qua trung điểm $BC$ hay ta có đpcm.
b) Dễ dàng chứng minh được tam giác LDP đồng dạng tam giác DIC theo trường hợp góc - góc
Suy ra $\dfrac{LD}{DI} = \dfrac{LP}{DC}$ hay $\dfrac{LD}{\dfrac12 DH} = \dfrac{2LQ}{LB}$ hay $\dfrac{DL}{DH} = \dfrac{LQ}{LB}$
Từ đó ta có tam giác LDH đồng dạng tam giác QLB theo trường hợp cạnh - góc - cạnh
Suy ra BQ vuông góc AL
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
