Bài 1: Cho tam giác ABC, 2 đường trung tuyến AM và BN cắt nhau tại G
a) S ABN= 1,5. S ABG
b) Cho S ABG=105 cm2. Tính S ABC
Thiên An - 2009
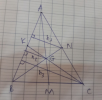
a)
Từ N và G kẻ đường vuông góc với AB lần lượt là h1 và h2
G là giao điểm 2 đường trung tuyến nên G là trọng tâm
[imath]h_1 // h_2(\text{cùng} \perp AB)[/imath]
Theo ta lét ta có :
[imath]\dfrac{h_2}{h_1}=\dfrac{BG}{BN}=\dfrac{2}{3}[/imath] (G là trọng tâm ABC)
Do đó,
[imath]\dfrac{S_{ABN}}{S_{ABG}}=\dfrac{\dfrac{1}{2}h_1.AB}{\dfrac{1}{2}h_2.AB}=\dfrac{h_1}{h_2}=\dfrac{1}{\dfrac{h_2}{h_1}}=1.5 \Rightarrow đpcm[/imath]
b)
Từ C kẻ đường vuông góc với AB là h3
Gọi K là giao điểm của CG với AB
[imath]h_3 // h_2(\text{cùng} \perp AB)[/imath]
Theo ta lét ta có :
[imath]\dfrac{h_2}{h_3}=\dfrac{GK}{CK}=\dfrac{1}{3}\text{ (G là trọng tâm ABC) }\Rightarrow h_3=3h_2[/imath]
Do đó ,
[imath]S_{ABC}=\dfrac{1}{2}h_3.AB=\dfrac{1}{2}.3.h_2.AB=3S_{ABG}=315(cm^2)[/imath]
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
