A
asroma11235
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Bài 1)
a) với
 , giải phương trình:
, giải phương trình:
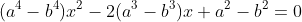
b)giải hệ phương trình:
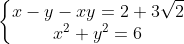
Bài 2:
a)tìm tất cả số nguyên dương n sao cho:
 chia hết cho
chia hết cho

b)Với 3 số x,y,z không âm thỏa mãn: x+y+z=6. Tìm min và max của:A=

Bài 3:
Trên đường tròn tâm O đường kính AB=2R lấy điểm N sao cho AN=R và m là 1 điểm bất kì trên cung nhỏ BN (M ko trùng với M,N). Gọi I là giao diểm của AM và BN. Đường thẳng đi qua điểm I và vuông góc với AB tại C.
a)Chứng minh 3 điểm M,M,C thẳng hàng
b)Xác định M để chu vi tứ giác ABMN lớn nhất
c)Chứng minh tâm đường tròn ngoại tiếp tam giác MNH luôn thuộc 1 đường thẳng cố định khi M thay đổi trên cunug nhỏ BN của đường trong (O;R).
d)Gọi P là điểm chính giữa cung AB không chứa N. Đường thẳng MP cắt AB tại D.Chứng minh:
 không đổi khi M thay đổi trên cung nhỏ BN.
không đổi khi M thay đổi trên cung nhỏ BN.
Bài 4:
Tìm tất cả các bộ ba số nguyên dương (x;y;z) thỏa mãn:
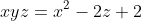
Bài 5:
Chứng minh rằng từ 53 số tự nhiên bất kì luôn chọn được 27 số mà tổng của chúng chia hết cho 27.
a) với
b)giải hệ phương trình:
Bài 2:
a)tìm tất cả số nguyên dương n sao cho:
b)Với 3 số x,y,z không âm thỏa mãn: x+y+z=6. Tìm min và max của:A=
Bài 3:
Trên đường tròn tâm O đường kính AB=2R lấy điểm N sao cho AN=R và m là 1 điểm bất kì trên cung nhỏ BN (M ko trùng với M,N). Gọi I là giao diểm của AM và BN. Đường thẳng đi qua điểm I và vuông góc với AB tại C.
a)Chứng minh 3 điểm M,M,C thẳng hàng
b)Xác định M để chu vi tứ giác ABMN lớn nhất
c)Chứng minh tâm đường tròn ngoại tiếp tam giác MNH luôn thuộc 1 đường thẳng cố định khi M thay đổi trên cunug nhỏ BN của đường trong (O;R).
d)Gọi P là điểm chính giữa cung AB không chứa N. Đường thẳng MP cắt AB tại D.Chứng minh:
Bài 4:
Tìm tất cả các bộ ba số nguyên dương (x;y;z) thỏa mãn:
Bài 5:
Chứng minh rằng từ 53 số tự nhiên bất kì luôn chọn được 27 số mà tổng của chúng chia hết cho 27.
Last edited by a moderator:

