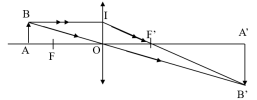
Nốt đề này để chuyển sang đề khác nha ^^
Câu 3:
Cho mạch điện như hình vẽ. Biết [imath]R_1 = 6 \Omega[/imath], [imath]R_2[/imath] là một biến trở, [imath]R_3 =15\Omega , R_4 = 10\Omega , R_5 = 1,25\Omega[/imath]. Đặt vào hai đầu A,B một hiệu điện thế không đổi U = 60V. Cho biết vôn kế là lý tưởng, các dây nối có điện trở không đáng kể và [imath]R_2 = 5\Omega[/imath]
a) Tính điện trở tương đương của mạch điện.
b) Tìm số chỉ của vôn kế.
c) Thay vôn kế bằng ampe kế có điện trở không đáng kể. Tìm giá trị của [imath]R_2[/imath] để công suất trên biến trở là cực đại và tìm giá trị công suất khi đó. |  |
Lời giải:
Sơ đồ mạch điện: [(R1 nt R3) // (R2 nt R4)] nt R5
a) Điện trở tương đương
R = [imath]\frac{(6+15).(10+5)}{6+15+10+5} + 1.25[/imath] = 10 ([imath]\Omega[/imath])
b) Số chỉ vôn kế đo độ lớn hiệu điện thế giữa hai đầu M,N => Uv = [imath]U_{MN}[/imath] = [imath]-U_1 + U_2[/imath]
Cường độ dòng điện mạch chính: [imath]I = \frac{U}{R} = \frac{60}{10} = 6(A)[/imath]
=> Hiệu điện thế hai đầu R1,R3: $U_{13} = U_{24} = U - I.R1 = 52,5 (V)
=> Cường độ qua R1: [imath]I_{13} =[/imath]\frac{52,5}{6+15}$ = 2,5 (A)
Tương tự tìm được cường độ dòng điện qua R2: $I_{24} = 3,5 (A)
=> $U_{MN} = -2,5x6 + 3,5x5 = 2,5 (V)
c) Sơ đồ mạch điện: (R1 // R2) nt (R3 // R4) nt R5
Gọi x là điện trở R2 cần tìm
Điện trở tương đương
R’ = [imath]\frac{6x}{6+x} + 6 + 1,25[/imath] = [imath]\frac{43.5+13.25x}{6+x}[/imath]
=> Cường độ dòng điện mạch chính: I’ = [imath]\frac{U}{R'}[/imath] = [imath]\frac{60(6+x)}{43,5+13,25x}[/imath]
=> Cường độ dòng điện qua R2: [imath]I_2[/imath] = I’.[imath]\frac{R_1}{R_1+R_2}[/imath] = [imath]\frac{360}{43,5+13,25x}[/imath]
=> Công suất tiêu thụ trên R2: [imath]P_2[/imath] = [imath]I_2^2[/imath].R2 = [imath]\frac{360^2}{\frac{43.5^2}{x}+1152.75+175.5625x}[/imath]
Để [imath]P_2[/imath]max, áp dụng BĐT Cauchy => x = 3,283 ([imath]\Omega[/imath])
Công suất [imath]P_2[/imath] = 56,2134 (W)
Câu 4:
Một thau nhôm khối lượng 0,5kg đựng 2kg nước ở [imath]20^o[/imath]C.
Thả vào thau nước một thỏi đồng khối lượng 200g lấy ra ở bếp lò. Nước nóng đến [imath]21,2^oC[/imath]. Tìm nhiệt độ của bếp lò? Biết nhiệt dung riêng của nhôm, nước, đồng lần lượt là: [imath]c_1 = 880J/kg.K, c_2=4200J/kg.K, c_3 =380J/kg.K[/imath]. Bỏ qua sự tỏa nhiệt ra môi trường.
a) Thực ra trong trường hợp này, nhiệt lượng tỏa ra môi trường là 10% nhiệt lượng cung cấp cho thau nước. Tìm nhiệt độ thực sự của bếp lò.
b) Nếu tiếp tục bỏ vào thau nước một thỏi nước đá có khối lượng 100g ở [imath]O^oC[/imath]. Nước đá có tan hết không? Tìm nhiệt độ cuối cùng của hệ thống. Biết nhiệt nóng chảy của nước đá là [imath]\lambda = 3,4.10^{5}[/imath] J/kg
Lời giải:
Đặt:
1 tương ứng thau nhôm, 2 tương ứng nước, 3 tương ứng thỏi đồng
a) Phương trình cân bằng nhiệt: [imath]Q_1 = Q_2[/imath]
⇔ [imath](m_1.c_1 + m_2.c_2).(t - t_{12}) = m_3.c_3.(t_3 - t)[/imath]
Thay các số tương ứng => [imath]t_3[/imath] = 160,779 độ C
b) Theo đề bài => Q1 + 10%.Q1 = Q2’
110%. [imath](m_1.c_1 + m_2.c_2).(t - t_{12})[/imath] = [imath]m_3.c_3.(t_3’ - t)[/imath]
=> [imath]t_3’[/imath] = 174,736 độ C
c) Gọi m là khối lượng của nước đá còn lại của hệ:
$$(m_1.c_1 + m_2.c_2 + m_3.c_3).(t - 0) = m.[imath]\lambda[/imath]
=> m = 0,556 (kg) > 0,1 kg
=> nước đá tan hết
Đề này khá đơn giản, nên hy vọng các bạn đều hiểu nhé!
*Toàn bộ bài làm đều thuộc về chị, nên nếu có sai sót các bạn vui lòng cho chị biết. Nếu reup vui lòng ghi nguồn: BQT Box Vật Lí - Hocmai Forum*
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
