Đáp án của đề này tới liền đây!!! Chắc phải tìm người type giùm chứ giải cả tháng trước mà giờ mới đăng lên cho mọi người được....
Câu I:
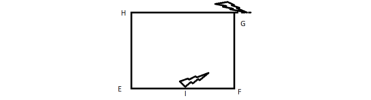
Trong một công viên có hai người đi xe đạp chuyển động đều dọc theo con đường hình vuông EFGH, chiều dài mỗi cạnh là 100m. Người thứ nhất xuất phát từ trung điểm I của cạnh EF, chuyển động hướng về F với vận tốc [imath]v_1 = 3m/s[/imath]. Người thứ hai xuất phát từ G, chuyển động hướng về H với vận tốc [imath]v_2 = 4 m/s[/imath] (Hình vẽ 1). Cả hai người xuất phát cùng lúc và đạp xe không quá 5 phút mỗi ngày.
1.1 Tìm khoảng cách giữa hai người đi xe đạp sau khi xuất phát 25 giây.
1.2 Kể từ lúc xuất phát, sau bao lâu hai người đi xe đạp gặp nhau tại E? Tính quãng đường mỗi người đi được | 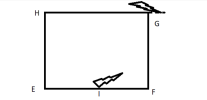 |
Hướng dẫn giải:
1.1
Đoạn đường người 1 đi được trong 25s:
[imath]S_{1} = 25.3 = 75 (m)[/imath]
[imath]\Rightarrow[/imath] Vị trí của người 1: nằm trên [imath]GF[/imath], cách [imath]F 25m[/imath] (như hình vẽ)
Tương tự tìm được vị trí của người 2: nằm tại H
[imath]\Rightarrow[/imath] khoảng cách: [imath]d = \sqrt[2]{75^{2}+100^{2}}=125m[/imath]
1.2
Thời gian người 1 tới E lần đầu: [imath]t_1 = \dfrac{350}{3}[/imath]
Các lần sau mất: thời gian đúng bằng một chu kì đi một vòng: [imath]t = \dfrac{400}{3}[/imath]
[imath]\Rightarrow T_{1}= \dfrac{350}{3} + n.\dfrac{400}{3}[/imath](n số vòng người 1 đạp)
Tương tự: [imath]T_{2}=50+m.100[/imath] (m là số vòng người 2 đạp)
Để 2 người gặp nhau tại E:
[imath]T_{1}=T_{2}[/imath]
[imath]\Rightarrow \dfrac{350}{3} + n.\dfrac{400}{3} = 50 + m.100[/imath]
Giải ra phương trình:
[imath]\frac{200}{3}= -100m+\frac{400}{3}n[/imath]
[imath]\Rightarrow[/imath] Cặp số nhỏ nhất thỏa (m;n)=(2;2)
[imath]\Rightarrow[/imath] Thời gian: [imath]T_{1}=T_{2}=\dfrac{350}{3}+2.\dfrac{400}{3}=383.33(s)[/imath]
Quãng đường người 1 đi: [imath]S_{1}= 383,33.3=1149,99 (m)[/imath]
Quãng đường người 2 đi: [imath]S_{2}= 383,33.4=1533,32 (m)[/imath]
Câu II:
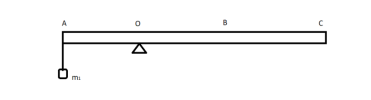
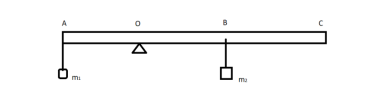
Một thước gỗ đồng chất, tiết diện đều có khối lượng 1 kg, chiều dàu AC = 60cm, được đặt trên giá đỡ tại O (hình vẽ 2). Đầu A của thước treo vật [imath]m_1[/imath] có khối lượng 1,2kg
2.1 Để thước cân bằng nằm ngang, phải treo vật [imath]m_2[/imath] tại điểm B có khối lượng bao nhiêu?
2.2 Tháo vật treo tại điểm B rồi treo vào điểm C vật [imath]m_3[/imath] có khối lượng 1 kg. Phía dưới điểm C có đặt một bình nước sao cho vật [imath]m_3[/imath] chìm hoàn toàn trong nước và không chạm đáy bình. Để thước cân bằng nằm ngang thì phải dịch chuyển giá đỡ của thước về phía C một đoạn bao nhiêu so với ban đầu? Biết khối lượng riêng của nước và vật treo tại C lần lượt là [imath]1000 kg/m^3[/imath] và [imath]5000 kg/m^3[/imath] |  |
Hướng dẫn giải:
[imath]CG=AG=30cm \Rightarrow OG=10cm[/imath]
Theo momen lực: Xét trục quay quanh O
[imath]\Longleftrightarrow m_{2}=0,6kg[/imath]
[imath]m_{1}g.OA = m_{2}g.OB+mg.OG[/imath]
[imath]\Rightarrow m_{2}=0,4kg[/imath]
Khi treo [imath]m_{3}[/imath] vào C thì: [imath]m_{3}g.OC + mg.OG > m_{1}g.OA[/imath]
Khi nhúng vào nước:
[imath]F_{3}=m_{3}.g-\frac{m_{3}}{D_{v}}.D_{n}.g=8(N)[/imath]
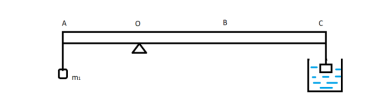
[imath]\Rightarrow[/imath] Để thanh cân bằng: Dịch O lại gần phía C hơn
TH1: [imath]x<10 \Rightarrow m_{1}gOA'=F_{3}.O'C+mg.O'G[/imath]
[imath]\Rightarrow[/imath] Vị trí O' lệch 6cm<10 (nhận)
TH2: [imath]x>10[/imath] [imath]\Rightarrow m_{1}gOA'=F_{3}.OC'+mg.O'G[/imath]
[imath]\Rightarrow[/imath] Vị trí của O' lệch [imath]-2cm\Rightarrow[/imath] loại
[imath]\Rightarrow[/imath] Dịch O lại gần C 6cm để đảm bảo cân bằng thỏa mãn yêu cầu bài toán
Hôm nay hai câu thôi nhé ^^
*Toàn bộ bài làm đều thuộc về mình, nên nếu có sai sót các bạn vui lòng cho mình biết. Nếu reup vui lòng ghi nguồn: BQT Box Vật Lí - Hocmai Forum* [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.