đề thi thử học mãi

L

luna_moonfang

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

giúp tớ một bài trong đề thi thử học mãi
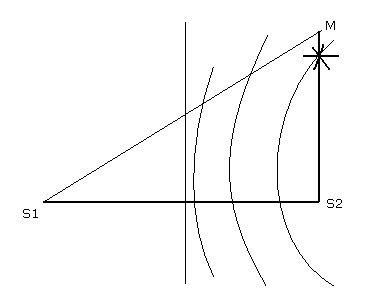
Có hai nguồn dao động kết hợp S1 và S2 trên mặt nước cách nhau 8 cm có phương trình dao động lần lượt là us1 = 2cos(10πt – π/4) mm và us2 = 2cos(10πt + π/4) mm. Tốc độ truyền sóng trên mặt nước là 10 cm/s. Xem biên độ của sóng không đổi trong quá trình truyền đi. Điểm M trên mặt nước cách S1 khoảng S1M = 10 cm và S2 khoảng S2M = 6 cm. Điểm dao động với biên độ cực đại trên S2M xa S2 nhất là
Chọn câu trả lời đúng:
A. 2,33 cm.
B. 3,57 cm.
C. 3,07 cm.
D. 6 cm.
bài này tớ đã xem thầy Hùng chữa rồi nhưng mà không hiểu lắm, mọi người giúp tớ nhé, cám ơn ạ :X
 
H

hocmai2704

Viết ptdđ tổng hợp => điểm dao động cực đại khi d1 - d2 = (k-1/4)lamda.
Với lamda = 2 cm.
Tại M => k =2,25.
Vậy M nằm giữa đường cực đại 2 và 3.
=> điểm cực đại gần M nhất ứng với k = 3. (vẽ tam giác S1S2M vuông tại S2 ra). Do M nằm giữa đường cực đại 2 và 3 nên đường cực dại 2 sẽ cắt S1m, đường cực đại 3 sẽ cắt S2M, do tính chất của hypebol, cho dù đường bậc 4 có cắt S2M thì điểm cắt cũng phải gần S2 hơn điểm cắt của đường bậc 3).
=> d1 - d2 = 5,5
Mặt khác, d1^2 - d2^2 = 64.
Giải ra đc d2 gần = 3,07 cm.
=> đ/án C.
 
Last edited by a moderator:
L

luna_moonfang

hocmai2704 said:
Viết ptdđ tổng hợp => điểm dao động cực đại khi d1 - d2 = (k-1/4)lamda.
Với lamda = 2 cm.
Tại N => k =2,25.
Vậy N nằm giữa điểm cực đại bậc 2 và 3.
=> điểm cực đại gần N nhất ứng với k = 3.
=> d1 - d2 = 5,5
Mặt khác, d2^2 - d1^2 = 64.
Giải ra đc d2 gần = 3,07 cm.
=> đ/án C.
Bấm để xem đầy đủ nội dung ...

cậu ơi, cho mình làm phiền cậu chút nữa nhé, mình không hiểu chỗ d1-d2 = (k -1/4)lamđa
tại sao lại có điều này hả cậu
với cả tại N k = 2,25 , điểm N là điểm nào hả cậu
với cả d2^2 - d1^2 = 64 nữa, mình cũng không hiểu chỗ này, hic, xin lỗi nhé, mình *** quá :((, trả lời dùm mình nhé
 
H

hocmai2704

Mình viết nhầm. d1^2 - d2^2 = 64 và M với N.
Giải thích:
Pt dao động tổng hợp:
[tex]u = 4cos(\frac{\pi(d1-d2)}{\lambda} + \frac{\pi}{4})(10\pi t - \frac {\pi(d1+d2)}{\lambda})[/tex]
điểm dao động với biên độ cực đại khi [tex]cos(\frac{\pi(d1-d2)}{\lambda} + \frac{\pi}{4}) = +-1[/tex]
=> [tex]d1 - d2 = (k-1/4)\lambda[/tex]
Ta có S1S2M vuông tại S2(pitago)
=>[tex]S1M-S2M<=d1-d2<=S1S2 => 2.25<=k<=4.25[/tex]
=> k=3 hoặc k =4 (đường cực đại 3 và 4 cắt S2M).
=> Cực đại cắt S2M gần M nhất(hay xa S2 nhất) trên đoạn S2M => k =3.
=>d1-d2 = 5,5.
và d1^2-d2^2 = 8^2(pitago) => đáp số.
 
Last edited by a moderator:
N

n0vem13er

untitled-24.jpg

mình cho bạn thêm 1 công thức để không phải tổng hợp dao động :

[TEX]d_1 - d_2 = (\Delta \varphi _M + \Delta \varphi ).\frac{\lambda }{2\pi }[/TEX]

với [TEX]\Delta \varphi _M[/TEX] là độ lệch pha tại điểm M đối với cả 2 nguồn mà bạn muốn

[TEX]\Delta \varphi [/TEX] là độ lệch pha của 2 nguồn [TEX](\Delta \varphi = \varphi _1 - \varphi _2)[/TEX]
trong bài này hai nguồn vuông pha , và chúng ta cần điểm M cùng pha với 2 nguồn, vì điểm M dao động cực đại

[TEX]d_1 - d_2 = (2k\pi - \frac{\pi }{2}).\frac{\lambda }{2\pi }[/TEX]

Mà ta có [TEX]10 - 6 <d_1 - d_2 < 8 - 0[/TEX]

[TEX]2,25 < k < 4,75[/TEX]

ta lấy k nguyên bé nhất = 3 vì k càng bé thì điểm cực đại cắt[TEX] S_2M[/TEX] của nó càng xa [TEX]S_2[/TEX]

[TEX]=> d_1 - d_2 = 5,5[/TEX]

[TEX]=> \sqrt{d_2^2 + 8^2} - d_2^2 = 5,5[/TEX]

[TEX]=> d_2 = 3,07 [/TEX]
 
Last edited by a moderator:
L

luna_moonfang

hay thật đấy, bạn làm trong có vài dòng à , cám ơn các bạn nhé :khi (67):
 
You must log in or register to reply here.
Top Bottom