Toán 8 Đề thi cuối HK II Trường THCS Thăng Long - Phòng GD&ĐT Ba Đình

[chi254]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Bài I (2 điểm) Giải các phương trinh sau:

1) [imath]2(2 x-1)-x=4[/imath]

2) [imath]\dfrac{x+1}{x-2}+\dfrac{1}{x}=\dfrac{5 x-4}{x^{2}-2 x}[/imath].

Bài II (2 điểm) Giải các bất phương trình sau và biểu diênn tập nghiệm trên trục số

1) [imath]3(x+2)>2 x-1[/imath]
2) [imath]\dfrac{x+1}{2}-\dfrac{3 x-5}{3} \geq \dfrac{x}{4}+3[/imath]

Bài III (2 điểm) Giải bài toán sau bằng cách lập phương trình:
Một xưởng dệt theo kế hoạch mỗi ngày phải dệt 30 áo. Thực tế xường đã dệt được mỗi ngày 40 áo nên đã hoàn thành trước thời hạn 3 ngày, ngoài ra còn dệt thêm được 20 chiếc áo. Tính số áo xưởng phải dệt theo kế hoạch?

Bài IV (3,5 diểm)
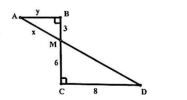
1) Tìm [imath]x[/imath]; [imath]y[/imath] trong hình vẽ bên
(Học sinh không phải vẽ lại hình)

2) Cho tam giác [imath]A B C[/imath] vuông tại [imath]A(AB<AC)[/imath], đường cao [imath]AH(H \in BC)[/imath].
a) Chứng minh : [imath]\triangle A B C[/imath] đồng dạng với [imath]\triangle H B A[/imath].
b) Lấy điểm [imath]M[/imath] thuộc [imath]AH[/imath]. Kẻ đường thẳng đi qua [imath]\mathrm{B}[/imath] và vuông góc với [imath]CM[/imath] tại [imath]K[/imath]. Chứng minh : [imath]CM . CK=CH.CB[/imath]
c) Tia [imath]BK[/imath] cắt HA tại D. Chứng minh: [imath]\widehat{B K H}=\widehat{B C D}[/imath].

Bài V [imath](0,5[/imath] điểm)
Giải bất phương trình sau [imath]3 x^{3}-5 x^{2}-x-2>0[/imath]

 

[chi254]

Đáp án:

Bài I:
1) [imath]2(2x - 1) - x = 4[/imath]
[imath]\iff 4x - 2 - x = 4[/imath]
[imath]\iff 3x = 6[/imath]
[imath]\iff x = 2[/imath]

Vậy phương trình có nghiệm là [imath]x =2[/imath]

2) ĐKXĐ: [imath]\begin{cases} x - 2 \neq 0 \\ x \ne 0 \\ x^2 - 2x \ne 0 \end{cases} \iff \begin{cases} x \ne 2 \\ x \ne 0 \end{cases}[/imath]

Ta có: [imath]\dfrac{x+1}{x-2}+\dfrac{1}{x}=\dfrac{5 x-4}{x^{2}-2 x}[/imath]

[imath]\iff \dfrac{x(x+1)}{x(x-2)} + \dfrac{x-2}{x(x-2)} = \dfrac{5x -4}{x^2 - 2x}[/imath]

[imath]\iff \dfrac{x^2 + x + x -2}{x^2 - 2x} = \dfrac{5x -4}{x^2 - 2x}[/imath]

[imath]\iff x^2 + 2x - 2 = 5x - 4[/imath]

[imath]\iff x^2 - 3x + 2 = 0[/imath]

[imath]\iff \left[\begin{matrix} x= 1 & & \\ x= 2 (Loại) & &\end{matrix}\right.[/imath]

Vậy phương trình có nghiệm [imath]x = 1[/imath]

Bài II:

1)
[imath]3(x +2) > 2x -1 \iff 3x + 6 > 2x - 1 \iff x > -7[/imath]

Vậy tập nghiệm của bất phương trình là: [imath](-7; + \infty)[/imath]

2) [imath]\dfrac{x+1}{2}-\dfrac{3 x-5}{3} \geq \dfrac{x}{4}+3[/imath]

[imath]\iff \dfrac{6(x+1)}{12} - \dfrac{4(3x -5)}{12} \ge \dfrac{3x}{12} + 3[/imath]

[imath]\iff \dfrac{6x + 6 -12x +20}{12} \ge \dfrac{3x + 36}{12}[/imath]

[imath]\iff \dfrac{-6x + 26}{12} \ge \dfrac{3x + 36}{12}[/imath]

[imath]\iff -6x + 26 \ge 3x + 36[/imath]

[imath]\iff 9x \le -10 \iff x \le \dfrac{-10}{9}[/imath]

Vậy tập nghiệm của bất phương trình là : [imath](-\infty; \dfrac{-10}{9})[/imath]

Bài III:

Một xưởng dệt theo kế hoạch mỗi ngày phải dệt 30 áo. Thực tế xường đã dệt được mỗi ngày 40 áo nên đã hoàn thành trước thời hạn 3 ngày, ngoài ra còn dệt thêm được 20 chiếc áo. Tính số áo xưởng phải dệt theo kế hoạch?

Gọi số áo xưởng phải dệt theo kế hoạch là [imath]x \ (x \in \mathbb{N^*})[/imath]

Số ngày dệt áo theo kế hoạch là: [imath]\dfrac{x}{30}[/imath]

Số áo dệt được theo thực tế là: [imath]x + 20[/imath]

Thời gian dệt áo theo thực tế là: [imath]\dfrac{x+20}{40}[/imath]

Do số ngày hoàn thành theo thực tế ít hơn dự định là 3 ngày nên: [imath]\dfrac{x +20}{40} + 3 = \dfrac{x}{30}[/imath]

[imath]\iff \dfrac{3(x +20)}{120} + \dfrac{360}{120} = \dfrac{4x}{120}[/imath]

[imath]\iff \dfrac{3x + 420}{120} = \dfrac{4x}{120}[/imath]

[imath]\iff 3x + 420 = 4x[/imath]

[imath]\iff x = 420[/imath]

Vậy số áo xưởng phải dệt theo kế hoạch là 420 cái áo

 

[chi254]

Bài IV:

Xét [imath]\Delta ABM[/imath] và [imath]\Delta DCM[/imath] có:
[imath]\widehat{ABM} = \widehat{DCM} = 90^o[/imath]
[imath]\widehat{AMB} = \widehat{DMC}[/imath] (đối đỉnh)
Suy ra: [imath]\Delta ABM \sim \Delta DCM[/imath] [imath](g-g)[/imath]
Suy ra: [imath]\dfrac{AB}{DC} = \dfrac{AM}{DM} = \dfrac{x}{\sqrt{6^2+8^2}} = \dfrac{x}{10}[/imath]
[imath]\iff \dfrac{y}{8} = \dfrac{x}{10} = k[/imath]
[imath]\to y = 8k; x = 10k[/imath]
Lại có: [imath]AB^2 + BM^2 = AM^2 \iff y^2 + 9 = x^2 \iff 64k^2 + 9 = 100k^2 \iff k = \dfrac{1}{2}[/imath]

Vậy [imath]x = 5; y = 4[/imath]

Bài V:

Bài VI [imath](0,5[/imath] điểm) Giải bất phương trình sau [imath]3 x^{3}-5 x^{2}-x-2>0[/imath]

[imath]\iff 3x^3 - 6x^2 + x^2 - 2x +x - 2 > 0[/imath]
[imath]\iff 3x^2(x - 2) + x(x -2) + (x-2) >0[/imath]
[imath]\iff (x -2)(3x^2 + x + 1) > 0[/imath]
Ta có: [imath]3x^2 + x + 1 = 3(x^2 + \dfrac{1}{3}x + \dfrac{1}{3}) = 3( (x + \dfrac{1}{6})^2 + \dfrac{11}{36} ) > 0[/imath]
Khi đó: BPT [imath]\iff x - 2 > 0 \iff x >2[/imath]

Vậy tập nghiệm của bpt là [imath](2;+\infty)[/imath]