Toán đề hình ôn tập hk 1 hình

[thao ly nguyen]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

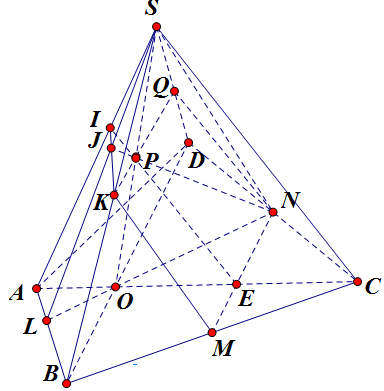
Cho hình chóp S.ABCD CÓ ĐÁY ABCD LÀ HÌNH BÌNH HÀNH TÂM O
1) TÌM GIAO TUYẾN CỦA HAI MẶT PHẲNG ( SAB) VÀ (SCD)
2) GỌI M,N,P,Q LẦN LƯỢT LÀ TRUNG ĐIỂM CỦA SB,SD,AM,AN
a) CM PQ//BD
b) Tìm thiết diện của ( AMN) với hình chóp
help me mai nộp rồi:r3

 

[vannguyenthicamvan821@gmail.com]

1.

• S = (SAB) [tex]\cap[/tex] (SCD)
• AB [tex]\subset[/tex] (SAB)
• CD [tex]\subset[/tex] (SCD)
• AB // CD

=> Giao tuyến của (SAB) và (SCD) là đt d đi qua S và d // AB // CD
2.
a. Trong [tex]\Delta[/tex] SBD có MN là đtb => MN // BD
Trong [tex]\Delta[/tex] AMN có PQ là đtb => PQ // MN
=> PQ // BD
b.

• A = (AMN) [tex]\cap[/tex] (ABCD)
• MN [tex]\subset[/tex] (AMN)
• BD [tex]\subset[/tex] (ABCD)
• MN // BD

=> Giao tuyến của (AMN) và (ABCD) là d' đi qua A và d' // MN // BD
Trong (SBC): d' cắt BC tại F, FM [tex]\cap[/tex] SC = J
Vậy thiết diện cần tìm là tứ giác AMJN

 

[Nguyệt Lam]

Đã gửi 15-09-2012 - 09:29


(MNP)$\cap$(SAB)
Gọi E là giao của AC, MN.
Trong (SAC): EP$\cap$ SA = I => I là điểm chung thứ nhất
Trong (ABCD): NO$\cap$AB = L
Trong (SNL):NP$\cap$SL= J
Mà NP$\subset$(SMN)
SL$\subset$(SAB)
=> J là điểm chung thứ 2
=> JI là giao tuyến cần tìm
(MNP)$\cap$(SCD)
N$\in$CD=> N là điểm chung thứ nhất
Trong (SAB): IJ cắt SB tại K.
Trong (SBD): KP cắt SD tại Q
Mà KP$\subset$(MNP)
=> QN là giao tuyến cần tìm