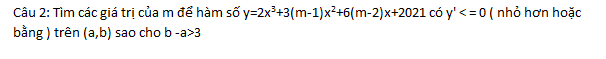Tìm các giá trị của [imath]m[/imath] để hàm số [imath]y = 2x^3 + 3(m-1)x^2 + 6(m-2)x + 2021[/imath] có [imath]y'\le 0[/imath] trên [imath](a;b)[/imath] sao cho [imath]b - a > 3[/imath]
Mọi người giúp mình câu này với ạ
Hoang Anh Tus[imath]y = 2x^3 + 3(m-1)x^2 + 6(m-2)x + 2021[/imath]
[imath]y'=6x^2+6(m-1)x+6(m-2)[/imath]
[imath]y'\le 0\Leftrightarrow x^2+(m-1)x+m-2\le 0[/imath]
[imath]\Leftrightarrow x^2-1+(m-1)x+(m-1)\le 0[/imath]
[imath]\Leftrightarrow (x-1)(x+1)+(m-1)(x+1)\le 0[/imath]
[imath]\Leftrightarrow (x+1)(x+m-2)\le 0[/imath] (1)
TH1: [imath]m-2=1\Rightarrow m=3[/imath] (1) đúng với mọi x (loại)
TH2: [imath]m-2>1\Rightarrow m>3[/imath]
(1)[imath]\Leftrightarrow 2-m<x<-1[/imath]
[imath]\Rightarrow x\in (2-m;-1)[/imath]
[imath]\Rightarrow b-a>3\Leftrightarrow -1+m-2>3\Rightarrow m>6[/imath]
Vậy [imath]m>6[/imath] thỏa ycbt
TH3: [imath]m-2<1\Rightarrow m<3[/imath]
(1)[imath]\Leftrightarrow -1<x<2-m[/imath]
[imath]\Rightarrow x\in (-1;2-m)[/imath]
[imath]\Rightarrow b-a>3\Leftrightarrow 2-m-1>3\Rightarrow m<-2[/imath]
Vậy [imath]m<-2[/imath] thỏa ycbt
Có gì khúc mắc em hỏi lại nhé
Ngoài ra em tham khảo thêm kiến thức tại đây nhé
https://diendan.hocmai.vn/threads/t...o-ban-hoan-toan-mien-phi.827998/#post-4045397
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.