- 24 Tháng mười 2018
- 1,616
- 1,346
- 216
- 25
- TP Hồ Chí Minh
- Đại học Sư phạm Kỹ thuật TP Hồ Chí Minh
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
I. chia khối lăng trụ tam giác bởi tam giác cắt 3 cạnh
- xét khối lăng trụ tam giác ABC.A'B'C' có thể tích là V. mặt phẳng (Q) cắt AA', BB', CC' lần lượt tại M, N, P thỏa mãn: [tex]\frac{AM}{AA'}=x; \frac{BN}{BB'}=y; \frac{CP}{CC'}=z[/tex]
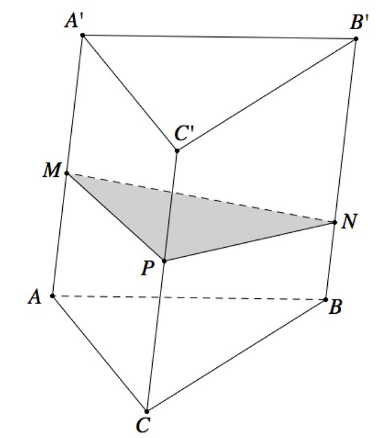
- khi đó, ta có:
[tex]V_{M.ABC}=\frac{x}{3}.V[/tex]
[tex]V_{M.BCPN}=\frac{y+z}{3}.V[/tex]
[tex]V_{ABC.MNP}=\frac{x+y+z}{3}.V[/tex]
II. cắt khối hộp bởi mặt phẳng
- xét khối hộp ABCD.A'B'C'D' có thể tích là V. ta cần nhớ:
[tex]V_{A'.BCD}=\frac{V}{6}[/tex]
[tex][/tex][tex]V_{B.A'B'C'}=\frac{V}{6}[/tex]
[tex][/tex][tex]V_{A'.C'BD}=\frac{V}{3}[/tex]
- giả sử mặt phẳng (S) cắt 4 cạnh AA'. BB', CC', DD' tại lần lượt 4 điểm thỏa mãn: [tex]\frac{AM}{AA'}=x;\frac{BN}{BB'}=y;\frac{CN}{CC'}=z;\frac{DQ}{DD'}=t[/tex].
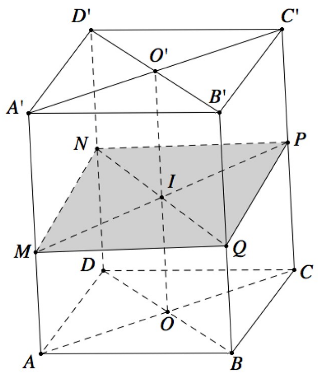
- khi đó ta có MNPQ là hình bình hành, và ta có đẳng thức sau:
[tex]x+z=y+t[/tex[/tex][tex]] [B] [tex]V_{ABCD.MNPQ}=\frac{x+y+z+t}{4}.V[/tex]
III. cắt khối chóp có đáy là hình bình hành bởi 1 mặt phẳng[/B]
- xét khối chóp S.ABCD có đáy ABCD là hình bình hành, măt phẳng (K) cắt 4 cạnh SA, SB, SC, SD lần lượt tại M, N, P, Q thỏa mãn: [tex]\frac{SM}{SA}=x;\frac{SN}{SB}=y;\frac{SP}{SC}=z;\frac{SQ}{SD}=t[/tex].
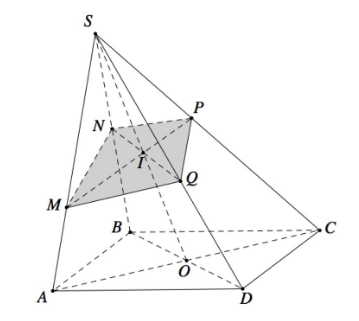
- khi đó, ta luôn có đẳng thức:
[tex]\frac{1}{x}+\frac{1}{z}=\frac{1}{y}+\frac{1}{t}[/tex]
[tex]V_{S.MNPQ}=\frac{xyzt}{4}(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}+\frac{1}{t}).V[/tex][/tex]
- xét khối lăng trụ tam giác ABC.A'B'C' có thể tích là V. mặt phẳng (Q) cắt AA', BB', CC' lần lượt tại M, N, P thỏa mãn: [tex]\frac{AM}{AA'}=x; \frac{BN}{BB'}=y; \frac{CP}{CC'}=z[/tex]

- khi đó, ta có:
[tex]V_{M.ABC}=\frac{x}{3}.V[/tex]
[tex]V_{M.BCPN}=\frac{y+z}{3}.V[/tex]
[tex]V_{ABC.MNP}=\frac{x+y+z}{3}.V[/tex]
II. cắt khối hộp bởi mặt phẳng
- xét khối hộp ABCD.A'B'C'D' có thể tích là V. ta cần nhớ:
[tex]V_{A'.BCD}=\frac{V}{6}[/tex]
[tex][/tex][tex]V_{B.A'B'C'}=\frac{V}{6}[/tex]
[tex][/tex][tex]V_{A'.C'BD}=\frac{V}{3}[/tex]
- giả sử mặt phẳng (S) cắt 4 cạnh AA'. BB', CC', DD' tại lần lượt 4 điểm thỏa mãn: [tex]\frac{AM}{AA'}=x;\frac{BN}{BB'}=y;\frac{CN}{CC'}=z;\frac{DQ}{DD'}=t[/tex].

- khi đó ta có MNPQ là hình bình hành, và ta có đẳng thức sau:
[tex]x+z=y+t[/tex[/tex][tex]] [B] [tex]V_{ABCD.MNPQ}=\frac{x+y+z+t}{4}.V[/tex]
III. cắt khối chóp có đáy là hình bình hành bởi 1 mặt phẳng[/B]
- xét khối chóp S.ABCD có đáy ABCD là hình bình hành, măt phẳng (K) cắt 4 cạnh SA, SB, SC, SD lần lượt tại M, N, P, Q thỏa mãn: [tex]\frac{SM}{SA}=x;\frac{SN}{SB}=y;\frac{SP}{SC}=z;\frac{SQ}{SD}=t[/tex].

- khi đó, ta luôn có đẳng thức:
[tex]\frac{1}{x}+\frac{1}{z}=\frac{1}{y}+\frac{1}{t}[/tex]
[tex]V_{S.MNPQ}=\frac{xyzt}{4}(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}+\frac{1}{t}).V[/tex][/tex]

