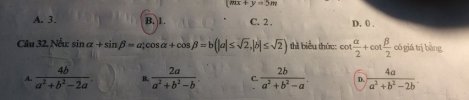nguyenthianh4c
Ta có: [imath](\cos \alpha+\cos \beta)^2+(\sin \alpha+\sin \beta)^2[/imath]
[imath]=2+2\cos \alpha.\cos \beta+2\sin \alpha.\sin \beta=2+2\cos (\alpha-\beta)=a^2+b^2[/imath]
[imath]\cot \dfrac{\alpha}{2}+\cot \dfrac{\beta}{2}=\dfrac{\cos \frac{\alpha}{2}}{\sin \frac{\alpha}{2}}+\dfrac{\cos \frac{\beta}{2}}{\sin \frac{\beta}{2}}[/imath]
[imath]=\dfrac{\sin (\frac{\alpha+\beta}{2})}{\sin \frac{\alpha}{2}.\sin \frac{\beta}{2}}=\dfrac{2\sin (\frac{\alpha+\beta}{2}).\cos (\frac{\alpha-\beta}{2})}{[\cos (\frac{\alpha-\beta}{2})-\cos (\frac{\alpha+\beta}{2})].\cos (\frac{\alpha-\beta}{2})}[/imath]
[imath]=\dfrac{\sin \alpha+\sin \beta}{\cos^2 (\frac{\alpha-\beta}{2})-\cos (\frac{\alpha+\beta}{2}).\cos (\frac{\alpha-\beta}{2})}[/imath]
[imath]=\dfrac{2(\sin \alpha+\sin \beta)}{1+\cos (\alpha-\beta)-(\cos \alpha+\cos \beta)}[/imath]
[imath]=\dfrac{4(\sin \alpha+\sin \beta)}{2+2\cos (\alpha-\beta)-2(\cos \alpha+\cos \beta)}=\dfrac{4a}{a^2+b^2-2b}[/imath]
Có gì khúc mắc em hỏi lại nhé
Ngoài ra em xem thêm tại
Công thức và bài tập lượng giác
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.