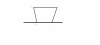
Một khối gỗ đồng chất, có chiều dày như nhau ở mọi điểm, có dạng hình thang cân ( hình 3.3.10). AB = 2 BC = 2CD = 2DA =30cm, có trọng lượng P=30N đặt trên mặt bàn nằm ngang.
a). Xác định trọng tâm của khối gỗ
b). Cần tác dụng vào B một lực F tối thiểu là bao nhiêu để khối gỗ bắt đầu quay quanh trục đi qua điểm C.
View attachment 178671
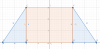
a) Mình sẽ dùng phương pháp tọa độ để tìm trọng tâm. Chia hình thanh thành 3 phần
Trong tâm tam giác ABC là: [TEX]x_1 = \frac{x_A+x_B+x_C}{3} = -10, y_1 = \frac{y_A + y_B + y_C}{3} = \frac{7,5}{\sqrt {3}}[/TEX], trọng lượng của nó là [TEX]P_1 = 5N[/TEX]
Trọng tâm hình chữ nhật BCFD là: [TEX]x_2 = 0, y_2 = \frac{7,5 \sqrt{3}}{2}[/TEX], trọng lượng của nó là [TEX]P_2 = 20N[/TEX]
Tương tự, trọng tâm tam giác DEF là: [TEX]x_3 = 10, y_3 = \frac{7,5}{\sqrt{3}}[/TEX], trọng lượng của nó là [TEX]P_3 = 5N[/TEX]
Công thức tính tọa độ trọng tâm là: [TEX]x = \frac{1}{P}. \sum x_i. P_i = \frac{1}{30}.(-10.5 + 0.20+ 10.5) = 0, y = \frac{1}{P}. \sum y_i. P_i = \frac{1}{30}.(5. \frac{7,5}{\sqrt{3}} + \frac{7,5\sqrt{3}}{2}.20+ 5.\frac{7,5}{\sqrt{3}}) = \frac{10}{\sqrt{3}}[/TEX]
Vậy trọng tâm nằm trên trục đối xứng của hình thang, cách đáy hơn hình thang [TEX]\frac{10}{\sqrt{3}}cm[/TEX]
b)
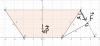
Áp dụng quy tắc momen tại thời điểm mà khối này quay:
[TEX]P.7,5 = F. 15 .\sin \alpha \rightarrow F = \frac{P}{2\sin \alpha}[/TEX]
Để F đạt nhỏ nhất thì [TEX]\sin \alpha[/TEX] phải lớn nhất [TEX]\rightarrow \alpha = 90^o \rightarrow F = \frac{P}{2} [/TEX]
Vậy phải tác dụng lực F một lực nhỏ nhất bằng P/2 theo hướng vuông góc với BC để vật quay quanh C.
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.