[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Mn giúp mik câu này vs
Vật lí 12 Cllx nằm nghiênh
- Thread starter leduymanh2005
- Ngày gửi
- Replies 1
- Views 268
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Hocmai Forum 
leduymanh2005
[imath]a/[/imath]
MÌnh giả sử trục [imath]Ox[/imath] có chiều trùng với chiều lò xo dãn nhé (chiều đi xuống mặt phẳng nghiêng)
Đổi: [imath]k= 1N/cm = 100N/m[/imath]
[imath]\omega = \sqrt{\dfrac{k}{m}}= 10\sqrt{5} \ rad/s[/imath]
Độ dãn của lò xo khi cân bằng: [imath]\Delta l_0 = \dfrac{mg\sin 30}{k}=0,01m=1cm[/imath]
Tại vị trí lò xo dãn [imath]x=2cm[/imath] (tức là cách vị trí cân bằng [imath]x_0 = x-\Delta l_0 =1cm[/imath] )thì có vận tốc là [imath]v_0 = 10\sqrt{15}cm/s[/imath], suy ra biên độ dao động:
[imath]A=\sqrt{x_0^2 + \dfrac{v_o^2}{\omega ^2}}=2cm[/imath]
[imath]b/[/imath]
Loading...
Chúc bạn học tốt!
-------
Xem thêm: Phương pháp chứng minh một vật dao động điều hòa
[imath]a/[/imath]
MÌnh giả sử trục [imath]Ox[/imath] có chiều trùng với chiều lò xo dãn nhé (chiều đi xuống mặt phẳng nghiêng)
Đổi: [imath]k= 1N/cm = 100N/m[/imath]
[imath]\omega = \sqrt{\dfrac{k}{m}}= 10\sqrt{5} \ rad/s[/imath]
Độ dãn của lò xo khi cân bằng: [imath]\Delta l_0 = \dfrac{mg\sin 30}{k}=0,01m=1cm[/imath]
Tại vị trí lò xo dãn [imath]x=2cm[/imath] (tức là cách vị trí cân bằng [imath]x_0 = x-\Delta l_0 =1cm[/imath] )thì có vận tốc là [imath]v_0 = 10\sqrt{15}cm/s[/imath], suy ra biên độ dao động:
[imath]A=\sqrt{x_0^2 + \dfrac{v_o^2}{\omega ^2}}=2cm[/imath]
| khi [imath]t=0[/imath] vật qua li độ [imath]1cm[/imath] theo chiều dương nên điểm pha ban đầu [imath]P_0[/imath] như hình vẽ. Phương trình dao động: [imath]x=2\cos (10\sqrt{5} t -\dfrac{\pi}{3}) cm[/imath] |  |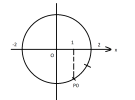
| Tại thời điểm [imath]t_1[/imath], vật qua vị trí lò xo không biến dạng. TH1: Xét vật đi theo chiều âm, điểm pha là [imath]P_1[/imath] như hình vẽ Từ [imath]t_1[/imath] đến [imath]t_2[/imath] điểm pha quét được góc là: [imath]\Delta \varphi = \omega .\dfrac{\pi}{4\sqrt{5}}=\dfrac{5\pi}{2}=2\pi + \dfrac{\pi}{2}[/imath] Điểm pha ở [imath]t_2[/imath] là [imath]P_2[/imath] Vậy tọa độ tại thời điểm này là [imath]x=-\dfrac{A\sqrt{3}}{2}=-\sqrt{3} cm[/imath] Quãng đường vật đi được từ [imath]t_1[/imath] đến [imath]t_2[/imath]: [imath]S = 4A + 1 + (2-\sqrt{3})=11-\sqrt{3} cm[/imath] Thời gian di chuyển: [imath]t=T + \dfrac{\dfrac{\pi}{2}}{\omega}[/imath] Tốc độ trung bình: [imath]v=\dfrac{S}{t} \approx 26,4cm/s[/imath] TH2: Vật đi theo chiều dương, điểm pha ở nửa dưới đường tròn. Trường hợp này bạn làm tương tự nhé |  |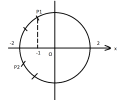
[imath]b/[/imath]
Loading...
Chúc bạn học tốt!
-------
Xem thêm: Phương pháp chứng minh một vật dao động điều hòa