[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
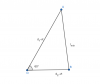
hai xe ô tô chuyển động thẳng đều cùng vận tốc, hướng tới điểm O trên 2 đường thẳng hợp với nhau 1 góc 60 độ. Ban đầu chúng cách O những khoảng d1=50km, d2=30km. xác định khoảng cách nhỏ nhất giữa 2 ô tô