Toán Chuyên đề: Vẽ thêm yếu tố phụ để giải các bài toán hình học

[braga]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

VẼ THÊM YẾU TỐ PHỤ ĐỂ GIẢI CÁC BÀI TOÁN HÌNH HỌC

I, Lời nói đầu:
Trong khi tìm phương pháp giải các bài toán hình học , có lúc việc vẽ thêm các yếu tố phụ làm cho việc giải bài toán trở nên dễ dàn hơn, thuận lợi hơn. Thậm chí có bài phải vẻ thêm yếu tố phụ mới tìm ra được lời giải . Tuy nhiên vẽ thêm yếu tố phụ như thế nào để có lợi cho bài toán là điều khó khăn và phức tạp.
Kinh nghiệm thực tế cho ta thấy rằng, không có phương pháp chung cho việc vẽ thêm các yếu tố phụ, mà là một sự sáng tạo trong khi giải toán, bởi vì việc vẽ thêm các yếu tố phụ cần đạt được mục đính là tạo điều kiện đẻgiair được bài toán 1 cách ngắn gọn chứ không phải là một côn việc tuỳ tiện, thích vẽ chỗ nào thì vẽ. Hơn nữa việc vẽ thêm yếu tố phụ phải tuân thủ theo các phép dựnh hình cơ bản và các bài toán dụng hình cơ bản.

II, Nhưng bài toán cơ bản:

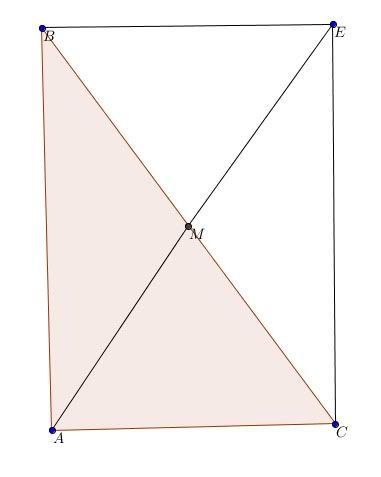
Bài 1: Cho tam giác ABC vuông tại A, M là trung điểm của cạnh BC. Chứng minh [TEX]AM=\frac{1}{2}BC[/TEX]




​

 

[harrypham]

Ủng hộ chuyên đề của Linh bằng cách sử dụng yếu tố phụ để giải bài 1 này.

Hướng suy nghĩ. Với chương trình hình lớp 7, ta học chủ yếu về việc chứng minh hai tam giác bằng nhau. Nên để chứng minh [TEX]AM= \frac{1}{2} BC[/TEX] ta phải đưa ra hai tam giác bằng nhau, trong đó có 1 cặp cạnh bằng nhau. Nhưng vì [TEX]AM= \frac{1}{2} BC[/TEX], nên ta sẽ vẽ thêm trên tia đối MA lấy E sao cho MA=ME. Như vậy đã có một mục đích: Chứng minh [TEX]AE=BC[/TEX].

Lời giải.

Trên tia đối tia MA lấy điểm E sao cho [TEX]MA=ME[/TEX].
Xét [TEX]\bigtriangleup ABM[/TEX] và [TEX]\bigtriangleup ECM[/TEX] có
+ [TEX]BM=MC[/TEX] (gt)
+ [TEX]AM=ME[/TEX] (gt)
+ [TEX]\widehat{BMA}= \widehat{CME}[/TEX] (đối đỉnh)
[TEX]\Rightarrow \bigtriangleup ABM= \bigtriangleup ECM[/TEX] (c.g.c)
[TEX]\Rightarrow AB=EC[/TEX] và [TEX]\widehat{ABM}= \widehat{ECM} \Rightarrow AB//EC[/TEX].

Do [TEX]AB//EC[/TEX] và [TEX]AB \perp AC[/TEX] nên [TEX]EC \perp AC \Rightarrow \widehat{ACE}=90^o= \widehat{BAC}[/TEX].

Xét [TEX]\bigtriangleup ACB[/TEX] và [TEX]ACE[/TEX] có
+ [TEX]AC[/TEX] chung
+ [TEX]AB=CE[/TEX] (cm trên)
+ [TEX]\widehat{ACE}= \widehat{BAC} \ (=90^o)[/TEX]
[TEX]\Rightarrow \bigtriangleup ACE= \bigtriangleup ACB[/TEX]
[TEX]\Rightarrow AE=BC \Rightarrow \fbox{AM= \frac{1}{2} BC }[/TEX].

 

[quangtrunghy95]

Trung tuyến ưng với cạnh huyền =1/2 cạch huyền bạn harrypham làm đúng về sau chung ta có thể áp dụng mà không cần cm

 

[braga]

Bài 2: Cho 2 tam giác ABC và A'B'C' có [TEX]\hat{BAC}+\hat{B'A'C'}=180^o, AB=A'B';AC=A'C'[/TEX]. M là trung điểm cạnh BC.

Chứng minh [TEX]AM=\frac{1}{2}B'C'[/TEX]

 

[harrypham]

Bài 2: Cho 2 tam giác ABC và A'B'C' có [TEX]\hat{BAC}+\hat{B'A'C'}=180^o, AB=A'B';AC=A'C'[/TEX]. M là trung điểm cạnh BC.

Chứng minh [TEX]AM=\frac{1}{2}B'C'[/TEX]

Bài này thì tương tự bài khi nãy thôi.
Dễ dàng chứng minh được [TEX]\bigtriangleup ABC= \bigtriangleup A'B'C'[/TEX] theo trường hợp c.g.c. Từ đó suy ra [TEX]BC=B'C'[/TEX]. Ta đúc y nguyên bài 1 vào để chứng minh [TEX]AM= \frac{1}{2}BC[/TEX], đồng nghĩa với việc [TEX]AM= \frac{1}{2}B'C'[/TEX].

 

[hocmaitoanhoc]

Góp cho pic 1 bài khó:
Bài 3: Cho góc xAy = 60 độ, Az là tia phân giác của góc xAy. Từ điểm B trên Ax vẽ đường thẳng song song với Ay cắt AZ tại C. Vẽ BD vuông góc với AY( D thuộc Ay)
Chứng minh [TEX]BD=\frac{1}{2}AC[/TEX]

 

[harrypham]

Góp cho pic 1 bài khó:
Bài 3: Cho góc xAy = 60 độ, Az là tia phân giác của góc xAy. Từ điểm B trên Ax vẽ đường thẳng song song với Ay cắt AZ tại C. Vẽ BD vuông góc với AY( D thuộc Ay)
Chứng minh [TEX]BD=\frac{1}{2}AC[/TEX]

Hướng suy nghĩ của mình cũng là kẻ thêm. Nhưng có vẻ khó hơn.

 

[braga]

Có thể vẽ hình như sau!



Gọi E là trung điểm của AC

Ta có: [TEX]\hat{A_1}=\hat{A_2}=30^o[/TEX]

[TEX]\hat{A_2}=\hat{C_1}(AD//BC) \Rightarrow \hat{A_1}=\hat{C_1} \Rightarrow \Delta ABC[/TEX] cân \Rightarrow [TEX]AB=CB[/TEX]

Xét [TEX]\Delta BAE[/TEX] và [TEX]\Delta BCE[/TEX] có:

[TEX]AB=CB \\\ AE=EC(gt) \\\ BE \ chung \\\ \Rightarrow \Delta BAE=\Delta BCE(c.c.c)[/TEX]

[TEX]\Rightarrow \hat{AEB}=\hat{CEB}[/TEX] mà [TEX]\hat{AEB}+\hat{CBE}=180^o \Rightarrow \hat{AEB}=90^o [/TEX]

[TEX]\Delta EBA[/TEX] có [TEX]\hat{AEB}=90^o ; \hat{A_1}=30^o \Rightarrow \hat{EBA}=60^o [/TEX]

[TEX]\Delta ADB[/TEX] có [TEX]\hat{ADB}=90^o ; \hat{DAB}=60^o \Rightarrow \hat{B_1}=30^o[/TEX]

Xét [TEX]\Delta DAB[/TEX] và [TEX]\Delta EBA[/TEX] có:

[TEX]\hat{DAB}=\hat{EBA}(=60^o) \\\ AB \ chung \\\ \hat{B_1}=\hat{A_1}(=30^o) \\\ \Rightarrow \Delta DAB=\Delta EBA(g.c.g) \Rightarrow BD=AE[/TEX]

Mà [TEX]AE=\frac{1}{2}BC \Rightarrow BD=\frac{1}{2}BC(dpcm) [/TEX]$.\square$
.

 

[braga]

Nếu vẽ hình như sau thì sao:



Mọi người thử nghĩ cách chứng minh [TEX]\Delta ABF=\Delta BAC[/TEX] coi có được không

 

[harrypham]

Nếu vẽ hình như sau thì sao:



Mọi người thử nghĩ cách chứng minh [TEX]\Delta ABF=\Delta BAC[/TEX] coi có được không

Hiển nhiên là [TEX]DF=BD[/TEX] nhỉ ? Ta cm theo cạnh góc cạnh thôi.

+ Chung AB
+ [TEX]\widehat{FBA}= \widehat{CAB}=30^o[/TEX]
+ [TEX]AC=FB[/TEX]

 

[hocmaitoanhoc]

Đề bài có cho AC=FB đâu, ta phải CM AC=FB chứ,.@-)@-)@-)@-)@-)

 

[harrypham]

Theo đề bài thì [tex]BD= \frac{1}{2} BC[/tex] nên có lẽ điểm F của braga được lây trên tia đối BD với FD=FB.
Như vậy thì FB=AC. Có điều này mới chứng minh được hai tam giác đó bằng nhau.

 

[hiensau99]

Bon chen :">. Đóng góp 1 bài

Cho tam giác ABC. Kẻ [TEX]AH \bot BC; \ H \in BC[/TEX]. Gọi M là trung điểm của BC. Biết AH và AM chia [TEX] \widehat{BAC}[/TEX] thành 3 phần bằng nhau. Tính các góc của tam giác ABC

 

[izamaek]

Mình thấy sau 1 vài bài, bạn có thể nêu 1 bí quyết vẽ thêm đường phụ ko?
Vd như khi cho AB có M là trung điểm, Cx cắt AB tại M, bí quyết cô mình đã dạy là vẽ Điểm E sao cho M là trung điểm CE

 

[harrypham]

Bon chen :">. Đóng góp 1 bài

Cho tam giác ABC. Kẻ [TEX]AH \bot BC; \ H \in BC[/TEX]. Gọi M là trung điểm của BC. Biết AH và AM chia [TEX] \widehat{BAC}[/TEX] thành 3 phần bằng nhau. Tính các góc của tam giác ABC

Ý Hiền là [TEX]\bigtriangleup AHB= \bigtriangleup AHM= \bigtriangleup ACM[/TEX] ?
Nếu thế thì từ [TEX]\bigtriangleup AHB= \bigtriangleup AHM[/TEX] suy ra [TEX]AH=AB[/TEX], [TEX]\bigtriangleup AHM= \bigtriangleup ACM[/TEX] suy ra [TEX]AH=AC[/TEX]. Từ đó chứng minh được [TEX]AB=AC[/TEX].

Như vậy [TEX]\bigtriangleup AMB= \bigtriangleup AMC[/TEX].
[TEX]\Rightarrow \widehat{AMB}= \widehat{AMC}[/TEX].
Và [TEX]\widehat{AMB}+ \widehat{AMC}=180^o[/TEX].
Nên [TEX]AM \bot BC[/TEX], như vậy [TEX]AM[/TEX] trùng AH.

Đo đó làm gì có chuyện chia ABC thành 3 phần bằng nhau.

 

[braga]

Mợi người cùng chém bài này đi !

Cho [TEX]\Delta ABC, AB<AC[/TEX] qua trung điểm D của cạnh BC
kẻ đường vuông góc với tia phân gíc của góc A cắt AB, AC lần lượt tại M , N.

a, Chứng minh BM=CN
b, Tím AM, BM theo AC=b, AB=c

 

[linhhuyenvuong]

Ý Hiền là [TEX]\bigtriangleup AHB= \bigtriangleup AHM= \bigtriangleup ACM[/TEX] ?
Nếu thế thì từ [TEX]\bigtriangleup AHB= \bigtriangleup AHM[/TEX] suy ra [TEX]AH=AB[/TEX], [TEX]\bigtriangleup AHM= \bigtriangleup ACM[/TEX] suy ra [TEX]AH=AC[/TEX]. Từ đó chứng minh được [TEX]AB=AC[/TEX].

Như vậy [TEX]\bigtriangleup AMB= \bigtriangleup AMC[/TEX].
[TEX]\Rightarrow \widehat{AMB}= \widehat{AMC}[/TEX].
Và [TEX]\widehat{AMB}+ \widehat{AMC}=180^o[/TEX].
Nên [TEX]AM \bot BC[/TEX], như vậy [TEX]AM[/TEX] trùng AH.

Đo đó làm gì có chuyện chia ABC thành 3 phần bằng nhau.

Chắc đây là chia góc!

Bon chen :">. Đóng góp 1 bài

Cho tam giác ABC. Kẻ [TEX]AH \bot BC; \ H \in BC[/TEX]. Gọi M là trung điểm của BC. Biết AH và AM chia [TEX] \widehat{BAC}[/TEX] thành 3 phần bằng nhau. Tính các góc của tam giác ABC

Kẻ ME vuông vs AC
Dễ dàng c/m: [tex]\large\Delta[/tex] AHM= [tex]\large\Delta[/tex] AEM (cạnh huyền-góc nhọn)
\Rightarrow [TEX]ME=HM=\frac{BM}{2}=\frac{MC}{2}[/TEX]
Tam giác MEC vuông tại E có [TEX]ME=\frac{MC}{2}[/TEX]
\Rightarrow [TEX]\hat{BCA}=30^o[/TEX]
\Rightarrow [TEX]\hat{ABC}=60^o[/TEX]
\Rightarrow [TEX]\hat{BAC}=90^o[/TEX]

 

[hiensau99]

Kẻ ME vuông vs AC
Dễ dàng c/m: [tex]\large\Delta[/tex] AHM= [tex]\large\Delta[/tex] AEM (cạnh huyền-góc nhọn)
\Rightarrow [TEX]ME=HM=\frac{BM}{2}=\frac{MC}{2}[/TEX]
Tam giác MEC vuông tại E có [TEX]ME=\frac{MC}{2}[/TEX]
\Rightarrow [TEX]\hat{BCA}=30^o[/TEX]
\Rightarrow [TEX]\hat{ABC}=60^o[/TEX]
\Rightarrow [TEX]\hat{BAC}=90^o[/TEX]

Kết quả của bạn đúng nhưng thiếu. Đây mới chỉ là trường hợp 1: AB<AC thôi. Còn trường hợp AB>AC cách tính tương tự chỉ khác: [TEX]\hat{BCA}=60^o[/TEX]; [TEX]\hat{ABC}=30^o[/TEX]; [TEX]\hat{BAC}=90^o[/TEX]

Bổ sung để có được [TEX]ME=HM=\frac{BM}{2}=\frac{MC}{2}[/TEX] thì bạn cần chứng minh thêm tam giác BAH=tam giác MAH (g.c.g)=> [TEX]HM=\frac{BM}{2}[/TEX]

 

[green_tran]

Anh đã lập một topic http://diendan.hocmai.vn/showthread.php?t=174797 nêu tính tổng quát của phương pháp này. Có lẽ có thể giúp các em một phần, hoặc ko giúp đc gì =))

 

[braga]

Mợi người cùng chém bài này đi !

Cho [TEX]\Delta ABC, AB<AC[/TEX] qua trung điểm D của cạnh BC
kẻ đường vuông góc với tia phân gíc của góc A cắt AB, AC lần lượt tại M , N.

a, Chứng minh BM=CN
b, Tím AM, BM theo AC=b, AB=c

1 tuần rồi, mà chưa ai làm được, bây giờ mình xin post lời giải.



Vẽ [TEX]BE//AC( E \in MN)[/TEX]

a, Xét [TEX]\Delta BED[/TEX] và [TEX]\Delta CND[/TEX] có:

[TEX]\hat{DBE}=\hat{DCN}(BE//CN) \\ BD=CD(gt) \\ \hat{BDE}=\hat{CDN}(DD) \\ \Rightarrow \Delta BED=\Delta CND(g.c.g) \Rightarrow BE=NC \ \ (1)[/TEX]

Xét [TEX]\Delta AIM[/TEX] và [TEX]\Delta AIN[/TEX] có:

[TEX]\hat{A_1}=\hat{A_2}(gt) \\ AD \ chung \\ \hat{ADM}=\hat{ADN}=90^o \\ \Rightarrow \Delta AIM=\Delta AIN(g.c.g) \Rightarrow \hat{AMN}=\hat{ANM} [/TEX]

Mà [TEX]\hat{ANM}=\hat{BEM}(BE//NC) \Rightarrow \hat{BME}=\hat{BEM}[/TEX]

[TEX]\Rightarrow \Delta MBE[/TEX] cân ở B [TEX]\Rightarrow BM=BE \ \ (2)[/TEX]

Từ (1) và (2) [TEX]\Rightarrow BM=NC[/TEX]

b, Ta có: [TEX]AB+BM=AN=AC-NC=AC-BM \Rightarrow 2BM=AC-AB[/TEX]

hay [TEX]2BM=b-c \Rightarrow \fbox{BM=\frac{b-c}{2}}(Do \ b>c)[/TEX]

[TEX]AM=AB=BM=c+\frac{b-c}{2}=\fbox{\frac{b+c}{2}}[/TEX]