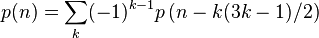Tin học Chuyên đề quy hoạch động

11thanhkhoeo · 30 Tháng sáu 2012

Quy hoạch động là một phương pháp rất hiệu quả để giải các bài toán tối ưu tổ hợp. ý tưởng cơ bản của phương pháp này là: để có lời giải của bài toán tối ưu kích thước n, ta giải các bài toán tương tự có kích thước nhỏ hơn và phối hợp lời giải của chúng để được lời giải của bài toán ban đầu. Đó chính là tư tưởng chia để trị một cách rất nghiêm ngặt.
Không phải bài toán nào cũng có thể giải bằng quy hoạch động. Để giải được bằng quy hoạch động, bài toán thoả mãn nguyên lý tối ưu Bellman: mọi dãy con của một dãy tối ưu cũng phải là dãy tối ưu.
Thông thường hàm mục tiêu của bài toán được xây dựng từ một hàm có dạng: f(n) = max(f(k)+g(n)), trong đó k là một số giá trị phù hợp nhỏ hơn n.
Hàm f(n) được gọi là hàm quy hoạch động. Việc tính giá trị hàm f được hiện từ dưới lên, tức là các giá trị n nhỏ được tính trước. Tất cả các kết quả được lưu vào bảng để phục vụ cho việc tính hàm quy hoạch động với các giá trị n lớn hơn.
Chúng ta sẽ xem xét một số bài toán quy hoạch động tiêu biểu để minh hoạ cho các tư tưởng trên.

11thanhkhoeo · 30 Tháng sáu 2012

1. Dãy con đơn điệu dài nhất
Cho dãy a1,a2,..an là dãy n số nguyên. Xoá đi một số phần tử của dãy trên và giữ nguyên trình tự của các phần tử còn lại thì ta được một dãy con của dãy ban đầu. Bài toán yêu cầu là xoá đi một số ít nhất các phần tử để dãy con thu được là dãy đơn điệu (chẳng hạn đơn điệu tăng). Yêu cầu này tương đương với yêu cầu chọn ra một số nhiều nhất các phần tử của dãy để dãy thu được (giữ nguyên thứ tự) là một dãy đơn điệu tăng.
Chẳng hạn dãy con tăng dài nhất của dãy 7 số hạng sau:
1 3 5 4 2 6 7
Là dãy con 1 3 5 6 7 có được từ việc xoá 2 phần tử 4 và 2 đi.
Để giải bài toán này bằng phương pháp quy hoạch động, ta trước hết phải xây dựng hàm quy hoạch động.
Gọi L(i) là độ dài dãy con đơn điệu tăng lớn nhất, có các phần tử lấy trong miền từ a1 đến ai và phần tử cuối cùng là ai.
Ta có công thức quy hoạch động như sau:
1. L(1) = 1
2. L(i) = max(1, L(j)+1 với mọi j<i và aj<=ai).
Chúng ta giải thích công thức như sau:
L(1)=1 là hiển nhiên.
Nếu ta không ghép ai vào dãy nào thì L(i)=1. Nếu ta ghép ai vào một dãy nào đó thì phải có một phần tử j đứng trước i, thoả mãn aj<=ai. Dãy con dài nhất có phần tử cuối cùng là aj có L(j) phần tử, vậy ghép thêm ai sẽ được dãy con có phần tử cuối cùng là ai và có L(j)+1 phần tử.
Trong tất cả các lựa chọn đó, ta chọn lựa chọn tối ưu nhất để tính L(i). Đó là nguyên nhân vì sao ta có hàm max.
Để cài đặt thuật toán ta dùng cấu trúc dữ liệu là một mảng 1 chiều L, L dùng lưu trữ giá trị tương ứng của L(i). Sự khác biệt giữa phương pháp quy hoạch động và chia để trị từ trên xuống là ở điểm này: các bài toán nhỏ được giải trước, và kết quả được lưu trữ lại để giải các bài toán lớn hơn. Cấu trúc dữ liệu dùng để lưu trữ các kết quả đó gọi là bảng phương án.

Mã:

procedure Optimize; var i,j; begin L[1] := 1; for i := 2 to n do begin L[i] := 1; for j := 1 to i-1 do if (a[j] <= a[i]) and (L[i] < L[j] + 1) then L[i] := L[j] + 1; end; end;

Sau khi tính xong hàm quy hoạch động, làm thế nào để tìm lại kết quả? Có 2 phương án. Phương pháp thứ nhất là dựa vào bảng phương án. Phương pháp thứ hai là xây dựng bảng truy vết.
Dựa trên bảng phương án ta sẽ tìm được phần tử có L lớn nhất. Đó chính là phần tử cuối cùng của dãy kết quả. Phần tử đứng ngay trước nó sẽ là phần tử j mà aj<ai và L=L[j]+1. Tìm được phần tử j đó, ta lại tìm được phần tử đứng ngay trước nó bằng phương pháp tương tự. Thủ tục lần vết tìm lại kết quả như sau:

Mã:

procedure Trace; begin i := 1; for j := 2 to n do if L[i] < L[j] then i := j; for k := L[i] downto 1 do begin kq[k] := i; for j := 1 to i do if (a[j]<=a[i]) and (L[i]=L[j]+1) then begin i := j; break; end; end; end;

mikelhpdatke · 1 Tháng bảy 2012

Mình cũng xin đóng góp một số bài

Bài toán chia kẹo
Có N gói kẹo, gói thứ i có Aicái kẹo. Không được bóc bất kỳ một gói kẹo nào, cần chia N gói kẹo thành haiphần sao cho độ chênh lệch số kẹo giữa hai gói là ít nhất.
Dữ liệu vào trong file "chiakeo.inp" có dạng :
- Dòng đầu tiên là số N(N<=100);
- Dòng thứ hai là N số Ai(i=1, 2,.., N; Ai <=100).
Kết quả ra file "chiakeo.out" có dạng:
- Dòng đầu là độ chênh lệchnhỏ nhất giữa hai phần có thể được.
- Dòng hai là một dãy N số,nếu si =1 thì gói thứ i thuộc phần 1, nếu si =2 thì góithứ i thuộc phần 2

Thuật toán:
Với một số M bất kì, nếu ta biếtđược có tồn tại một cách chọn các gói kẹo để tổng số kẹo của các gói được chọnbằng đúng M không, thì bài toán được giải sẽ quyết. Vì đơn giản là ta chỉ cầnchọn số M sao cho M gần với Ai/2nhất (với i =1,2,..,N). Sau đó xếp các gói kẹo để tổng bằng M vào phần một,phần thứ hai sẽ gồm các gói kẹo còn lại. Để kiểm tra được điều trên ta sẽ xâydựng tất cả các tổng có thể có của N gói kẹo bằng cách: ban đầu chưa có tổngnào được sinh ra. Làm lần lượt với các gói kẹo từ 1 đến N, với gói kẹo thứ i,ta kiểm tra xem hiện tại có các tổng nào đã được sinh ra, giả sử các tổng đó làx1, x2,.., xt vậy thì đến bước này sẽ có thểsinh ra các tổng x1, x2,.., xt và Aivà x1+Ai,x2+Ai,..,xt+Ai.Với N gói kẹo, mà mỗi gói có không quá 100 cái kẹo vậy tổng số kẹo không vượtquá N*100 <= 10000 cái kẹo. Dùng mảng đánh dấu D, nếu có thể sinh được ratổng bằng k thì D[k] = 1 ngược lại D[k] = 0.
Chương trình thể hiện thuật toántrên.

Mã:

{$A+,B-,D+,E+,F-,G-,I+,L+,N-,O-,P-,Q+,R+,S+,T-,V+,X+,Y+}
{$M 16384,0,655360}
Program chia_keo;
uses crt;
const max = 100;
fi ='chiakeo.inp';
fo ='chiakeo.out';
var a,s : array[1..max]of integer;
d1,d2,tr : array[0..max*max]of integer;
n,m,sum : integer;
Procedure docf;
var f: text;
k : integer;
begin
assign(f,fi); reset(f);
readln(f,n);
sum:=0;
for k:=1 to n do
begin
read(f,a[k]);
sum:=sum+a[k];
end;
close(f);
end;
Procedure lam;
var i,j : integer;
Begin
fillchar(d1,sizeof(d1),0);
fillchar(tr,sizeof(tr),0);
d1[0]:=1;d2:=d1;
for i:=1 to n do
begin
   for j:=0 to sum-a[i] do
       if (d1[j]=1)and(d2[j+a[i]]=0) then
                 begin
                       d2[j+a[i]]:=1;
                         tr[j+a[i]]:=i;
                 end;
       d1:=d2;
end;
end;
Procedure ghif;
var m,k : integer;
f :text;
Begin
fillchar(s,sizeof(s),0);
m:=sum div 2;
while d2[m]=0 do dec(m);
assign(f,fo);
rewrite(f);
writeln(f,sum-2*m);
while tr[m]>0 do
begin
s[tr[m]]:=1;
m:=m-a[tr[m]];
end;
for k:=1 to n do write(f,k+1,#32);
close(f);
end;
BEGIN {main}
docf;
lam;
ghif;
END.

Nhận xét:Chương trình trên đây cài đặt rất "thô", song dễ hiểu. Chương trình có thể cảitiến lại để có thể chạy được số liệu lớn hơn, nhanh hơn. Ví dụ: bạn có cần để ýđến các tổng >sum/2 không? Có thể tích hợp cả ba mảng D1, D2 và TR làm mộtmảng không? Bạn đọc hãy chỉnh lại để chương trình chạy tốt hơn.

11thanhkhoeo · 1 Tháng bảy 2012

2. Xâu con chung dài nhất
Cho 2 xâu X,Y. Hãy tìm một xâu S thoả mãn:
1. S có thể nhận được từ X,Y bằng cách xoá đi một số kí tự (tức là S là xâu con của X và của Y).
2. Độ dài của S là lớn nhất.
Trước hết ta xây dựng hàm quy hoạch động:
Gọi L(i,j) là độ dài xâu con chung dài nhất của xâu X (i) gồm i kí tự phần đầu của X (X (i) = [1..i]) và xâu Y(j) gồm j kí tự phần đầu của Y (Y(j) = [1..j]).
Ta có công thức quy hoạch động như sau:
1. L(0,j)=L(i,0)=0.
2. L(i,j) = L(i1,j1)+1 nếu X = Y[j].
3. L(i,j) = max(L(i1,j), L(i,j1)) nếu X <> Y[j].
Công thức 1. là hiển nhiên. Công thức 2 và 3 được hiểu như sau: Nếu X =Y[j] thì ta sẽ chọn ngay cặp phần tử đó, đoạn còn lại của 2 xâu là X [ 1..i1] và Y[1..j1] có xâu con chung dài nhất L(i1,j1) phần tử, vậy X (i) và Y(j) có xâu con chung dài nhất L(i1,j1)+1.
Ngược lại, nếu X <> Y[j] thì ta có 2 giải pháp: hoặc bỏ qua X và so X (i-1) với Y(j). Cách đó cho xâu con dài nhất L(i-1,j) phần tử. Ngược lại, ta có thể bỏ qua Y[j] và so X (i) với Y(j-1) để có xâu con dài nhất L(i,j-1) phần tử. Trong 2 cách chọn ta sẽ chọn cách tối ưu hơn.
Bảng phương án của ta sẽ là một bảng 2 chiều L[0..m,0..n], với n,m lần lượt là độ dài của X và Y. Chương trình con tính bảng phương án như sau:

Mã:

procedure Optimize; var i,j; begin for i := 0 to m do L[i,0] := 0; for j := 0 to n do L[0,j] := 0; for i := 1 to m do for j := 1 to n do if X[i]=Y[j] then L[i,j] := L[i-1,j-1]+1 else L[i,j] := max(L[i-1,j],L[i,j-1]]); end;

Để lần vết tìm nghiệm, ta dựa trên bảng phương án. Xâu con chung lớn nhất của X,Y có độ dài L[m,n]. Dựa vào tương quan giá trị giữa L[i,j], L[i1,j], L[i,j1] và L[i1,j1] ta sẽ biết trong quá trình quy hoạch động ta đã chọn hướng đi nào:

Mã:

procedure Trace; begin i := m; j := n; repeat if X[i]=Y[j] then begin kq[i] := 1; i:=i-1; j:=j-1; end else if L[i,j]=L[i-1,j] then i:=i-1 else j:=j-1; until (i=0) or (j=0); S := ''; for i:=1 t m do if kq[i]=1 then S:=S+X[i]; end;

Dễ dàng kiểm tra thuật toán quy hoạch động tìm xâu con chung dài nhất có độ phức tạp tính toán là O(n2) và đòi hỏi không gian bộ nhớ cũng là O(n2).

mikelhpdatke · 1 Tháng bảy 2012

BÀI TOÁN CÁI TÚI

Trong siêu thị có n gói hàng (n <= 100), gói hàng thứ i có trọng lượng là Wi <= 100 và trị giá Vi <= 100. Một tên trộm đột nhập vào siêu thị, sức của tên trộm không thể mang được trọng lượng vượt quá M ( M <= 100). Hỏi tên trộm sẽ lấy đi những gói hàng nào để được tổng giá trị lớn nhất.
Cách giải:
Nếu gọi B[i, j] là giá trị lớn nhất có thể có bằng cách chọn trong các gói {1, 2, ..., i} với giới hạn trọng lượng j. Thì giá trị lớn nhất khi được chọn trong số n gói với giới hạn trọng lượng M chính là B[n, M].
1. Công thức truy hồi tính B[i, j].
Với giới hạn trọng lượng j, việc chọn tối ưu trong số các gói {1, 2, ...,i - 1, i} để có giá trị lớn nhất sẽ có hai khả năng:
• Nếu không chọn gói thứ i thì B[i, j] là giá trị lớn nhất có thể bằng cách chọn trong số các gói {1, 2, ..., i - 1} với giới hạn trọng lượng là j. Tức là
B[i, j] = B[i - 1, j]
• Nếu có chọn gói thứ i (tất nhiên chỉ xét tới trường hợp này khi mà Wi  j) thì B[i, j] bằng giá trị gói thứ i là Vi cộng với giá trị lớn nhất có thể có được bằng cách chọn trong số các gói {1, 2, ..., i - 1} với giới hạn trọng lượng j - Wi. Tức là về mặt giá trị thu được:
B[i, j] = Vi + B[i - 1, j - Wi]
Vì theo cách xây dựng B[i, j] là giá trị lớn nhất có thể nên nó sẽ là max trong 2 giá trị thu được ở trên.
2. Cơ sở quy hoạch động:
Dễ thấy B[0, j] = giá trị lớn nhất có thể bằng cách chọn trong số 0 gói = 0.
3. Tính bảng phương án:
Bảng phương án B gồm n + 1 dòng, M + 1 cột, trước tiên được điền cơ sở quy hoạch động: Dòng 0 gồm toàn số 0. Sử dụng công thức truy hồi, dùng dòng 0 tính dòng 1, dùng dòng 1 tính dòng 2, v.v... đến khi tính hết dòng n.

0 1 ... M
0
0 0 0 0
1
2
... ...
n
4. Truy vết:
Tính xong bảng phương án thì ta quan tâm đến b[n, M] đó chính là giá trị lớn nhất thu được khi chọn trong cả n gói với giới hạn trọng lượng M. Nếu b[n, M] = b[n - 1, M] thì tức là không chọn gói thứ n, ta truy tiếp b[n - 1, M]. Còn nếu b[n, M]  b[n - 1, M] thì ta thông báo rằng phép chọn tối ưu có chọn gói thứ n và truy tiếp b[n - 1, M - Wn]. Cứ tiếp tục cho tới khi truy lên tới hàng 0 của bảng phương án.

Mã:

program The_Bag;
const
  max = 100;
var
  W, V: Array[1..max] of Integer;
  B: array[0..max, 0..max] of Integer;
  n, M: Integer;

procedure Enter;            {Nhập dữ liệu}
var
  i: Integer;
begin
  Write('n = '); Readln(n);
  for i := 1 to n do
    begin
      Writeln('Pack ', i);
      Write('  + Weight : '); Readln(W[i]);
      Write('  + Value  : '); Readln(V[i]);
    end;
  Write('M = '); Readln(M);
end;

procedure Optimize;    {Tính bảng phương án bằng công thức truy hồi}
var
  i, j: Integer;
begin
  FillChar(B[0], SizeOf(B[0]), 0);    {Điền cơ sở quy hoạch động}
  for i := 1 to n do
    for j := 0 to M do
      begin
        B[i, j] := B[i - 1, j];        {Giả sử không chọn gói thứ i thì B[i, j] = B[i - 1, j]}
        {Sau đó đánh giá: nếu chọn gói thứ i sẽ được lợi hơn thì đặt lại B[i, j]}
        if (j >= W[i]) and (B[i, j] < B[i - 1, j - W[i]] + V[i]) then
          B[i, j] := B[i - 1, j - W[i]] + V[i];
      end;
end;

procedure Trace;        {Truy vết tìm nghiệm tối ưu}
begin
  Writeln('Max Value : ', B[n, M]);    {In ra giá trị lớn nhất có thể kiếm được}
  Writeln('Selected Packs: ');
  while n <> 0 do        {Truy vết trên bảng phương án từ hàng n lên hàng 0}
    begin
      if B[n, M] <> B[n - 1, M] then    {Nếu có chọn gói thứ n}
        begin
          Writeln('Pack ', n, ' W = ', W[n], ' Value = ', V[n]);
          M := M - W[n];    {Đã chọn gói thứ n rồi thì chỉ có thể mang thêm được trọng lượng M - Wn nữa thôi}
        end;
      Dec(n);
    end;
end;

begin
  Enter;
  Optimize;
  Trace;
end.

mikelhpdatke · 2 Tháng bảy 2012

Bài toán biến đổi xâu

Cho xâu ký tự X, xét 3 phép biến đổi:
a) Ínerrt(i, C): i là số, C là ký tự: Phép Insert chèn ký tự C vào sau vị trí i của xâu X.
b) Replace(i, C): i là số, C là ký tự: Phép Replace hay ký tự tại vị trí i của xâu X bởi
ký tự C.
c) Delete(i): i là số, phép Delete xóa ký tự tại vị trí i của xâu X.

Yêu cầu:

Cho trước xâu X, Y hãy tìm ít nhất một số phép biến đổi xâu X thành xâu Y

Input: Dữ liệu vào file STR.INP

Dòng 1: Chứa xâu X (độ dài <=100)
Dòng 2: Chưa xâu Y (đồ dài <=100)

Output: Dữ liệu vào file STR.OUT

Ghi các phép biến đổi cần thực hiện để chuyển xâu X -> Y

Đối với xâu ký tự thì việc xoá, chèn sẽ làm cho các phần tử phía sau vị trí biến đổi bị đánh chỉ số lại, gây khó khăn cho việc quản lý vị trí. Để khắc phục điều này, ta sẽ tìm một thứ tự biến đổi thoả mãn: Phép biến đổi tại vị trí i bắt buộc phải thực hiện sau các phép biến đổi tại vịtrí i + 1, i + 2, …
Ví dụ: X = 'ABCD'; I nsert(0, E) sau đó Delete(4) cho ra X = 'EABD'. Cách này không tuân thủ nguyên tắc
Delete(3) sau đó Insert(0, E) cho ra X = 'EABD'. Cách này tuân thủnguyên tắc đềra. Nói tóm lại ta sẽtìm một dãy biến đổi có vịtrí thực hiện giảm dần.

{-------------------------------------------}

CTTH:
Gọi F[i,j] là số phép biến đổi tối thiểu để biến đổi i ký tự đầu của xâu X thành j ký tự đầu của xâu Y.
Ta xét 2 trường hợp chính
*TH1: X=Y[j] thì F[i,j]:=F[i-1,j-1]. Số phép biến đổi xâu này sẽ = số phép biến đổi của F[i-1,j-1].
*TH2: X<>Y[j].
Ta chia thành các trường hợp nhỏ:
- Nếu chèn 1 phần tử = Y[j] vào sau vị trí i của xâu X. Thì F[i,j]:=F[i,j-1];
- Nếu xóa 1 phần tử thứ i trong xâu X. Thì F[i,j]:=F[i-1,j];
- Nếu thay 1 phần tử thứ i trong xâu X = phần tử thứ j trong xâu Y thì
F[i,j]:=F[i-1,j-1];

Vây ta có CTTH:
[TEX] F[i,j]:= \Left{\begin{ F[i,j]:=F[i-1,j-1] <=> X[i]=Y[j] }\\{ F[i,j]:=Min(F[i-1,j],F[i,j-1],F[i-1,j-1]) + 1 <=> X[i]<>Y[j]} [/TEX]

Cơ sở QHĐ:
F[i,0]:=i;
F[0,j]:=j;

Truy viết :
Nếu X[m]=Y[n] thì truy tiếp F[m-1,n-1];
Nếu ko:
- Nếu F[m,n]=F[m-1,n]+1 thì phép sử dụng là Delete(m);
- Nếu F[m,n]=F[m,n-1]+1 thì phép sử dụng là Insert(m,Y[n]);
- Nếu F[m,n]=F[m-1,n-1]+1 thì phép sử dụng là Replace(m,Y[n]);
Khi về 0,0 thì kết thúc

Mã:

Program BIENDOIXAU; Var X,Y:String; m,n:integer; F:array[-1..101,-1..101] Of Integer; Function Min(a,b,c:integer):Integer; Begin If a>b then min:=b else min:=a; if min>c then min:=c; end; Procedure Init; Var i,j:integer; Begin Readln(X); READLN(Y); m:=Length(X); n:=length(Y); For i:=0 to m do F[i,-1]:=101; For j:=0 to n do F[-1,j]:=101; For i:=1 to m do F[i,0]:=i; For j:=1 to n do F[0,j]:=j; For i:=1 to M do For j:=1 to N do Begin If X[i]=Y[j] then F[i,j]:=F[i-1,j-1]; If X[i]<>Y[j] then F[i,j]:=Min(F[i-1,j],F[i,j-1],F[i-1,j-1])+1; End; writeln(F[m,n]); End; Procedure Trace; Var i,j:integer; Begin While (m<>0) or (n<>0) do If X[m]=Y[n] then Begin dec(m); dec(n); End Else Begin Write(X,' ->'); If F[m,n]=F[m,n-1]+1 then Begin Writeln('Insert(',m,', ',Y[n],' )'); Insert(Y[n],X,m+1); dec(n); End Else If F[m,n]=F[m-1,n-1]+1 then Begin writeln('Replace(',m,', ',Y[n],')'); X[m]:=Y[n]; dec(n); dec(m); End Else Begin writeln('Delete(',m, ')'); Delete(X,m,1); dec(m); End; writeln('->', X); End; End; BEGIN init; Trace; readln END.

11thanhkhoeo · 4 Tháng bảy 2012

bài toán cái túi

Thật vậy, gọi F(i,j) là giá trị lớn nhất thu được khi ta được chọn i đồ vật từ 1 đến i để xếp vào balô có trọng tải j. Dễ thấy là F(0,j) = F(i,0)=0. Nếu i,j>0 thì ta thấy:
- trường hợp thứ nhất: j<wi. Khi đó ta không thể đưa vật i vào balô, và giá trị lớn nhất thu được sẽ là chọn i-1 vật còn lại và trọng tải balô vẫn là j, tức là F(i,j)=F(i-1,j).
- trường hợp thứ hai: j>=wi. Trong tình huống này ta có thể chọn vật i để đưa vào balô hoặc không. Nếu không chọn thì F(i,j)=F(i-1,j) như trường hợp trên. Nếu chọn thì F(i,j)=F(i-1,j-wi) + vi. Công thức này rất dễ hiểu, vì khi ta chọn vật i thì tải trọng của balô còn lại là j-wi, ta còn i-1 vật nữa để chọn nên giá trị lớn nhất thu được là F(i-1,j-wi) + vi. Trong 2 cách đó ta sẽ chọn cách tốt hơn. Vậy F(i,j)=max(F(i-1,j-wi) + vi, F(i-1,j)).
Công thức quy hoạch động có thể tóm tắt lại như sau:
1. F(0,j) = F(i,0)=0
2. F(i,j) = F(i-1,j) nếu j<wi
3. F(i,j)=max(F(i-1,j-wi) + vi, F(i-1,j)) nếu j>=wi.
Chương trình con tính bảng phương án sẽ thực hiện tính các giá trị i,j từ nhỏ đến lớn. Cụ thể như sau:

Mã:

procedure Optimize;
begin 
    for i := 0 to n do F[i,0]:=0;
    for j := 0 to m do F[0,m]:=0;
    for i := 1 to n do begin 
        for j := 1 to m do 
            if j<w[i] then F[i,j] := F[i-1,j]
            else    
                F[i,j] := max(F[i-1,j], F[i-1,j-w[i]]+v[i]);
    end;
end;

Sau quá trình tính toán, giá trị lớn nhất thu được khi được chọn n đồ vật với balô trọng tải m sẽ là F[n,m]. Quá trình lần vết dựa vào tương quan giữa F[i,j], F[i-1,j] và F[i-1,j-w]+v sẽ xác định được các vật được chọn. Độc giả có thể dễ dàng xây dựng chương trình con truy vết và chứng minh được thuật giải quy hoạch động này có độ phức tạp tính toán là O(n.m). Chi phí bộ nhớ cũng là O(n.m).
Trong phần sau trình bày về những cải tiến đối với quy hoạch động, chúng tôi sẽ trình bày những cách cài đặt các thuật toán trên với chi phí bộ nhớ thấp hơn.

mikelhpdatke · 19 Tháng bảy 2012

Trong chuyên đề này có bài trò chơi với băng số, khá hay

Trò chơi với băng số là trò chơi tham gia trúng thưởng được mô tả như sau: Có một băng hình chữ nhật được chia ra làm n ô vuông, đánh số từ trái qua phải bắt đầu từ 1. Trên ô vuông thứ i người ta ghi một số nguyên dương ai, i = 1, 2, ..., n. Ở một lượt chơi, người tham gia trò chơi được quyền lựa chọn một số lượng tùy ý các ô trên băng số. Giả sử theo thứ tự từ trái qua phải, người chơi lựa chọn các ô i1, i2, ..., ik. Khi đó điểm số mà người chơi đạt được sẽ là:

ai1 - ai2 + ... + (-1)k-1aik

Yêu cầu: Hãy tính số điểm lớn nhất có thể đạt được từ một lượt chơi.
Dữ liệu:

Dòng đầu tiên chứa số nguyên dương n ( n ≤ 106 ) là số lượng ô của băng số;

Dòng thứ hai chứa n số nguyên dương a1, a2, ..., an ( ai ≤ 104, i = 1, 2, ..., n ) ghi trên băng số. Các số liên tiếp trên cùng dòng được ghi cách nhau bởi ít nhất một dấu cách.

Kết quả:

Một số nguyên duy nhất là số điểm lớn nhất có thể đạt được từ một lượt chơi.

Ví dụ:

Dữ liệu ............Kết quả

7
4 9 2 4 1 3 7 .........17

Giải:
F[i,+] là điểm lớn nhất khi chọn trong giới hạn i số đầu và dấu cuối cùng là '+'
F[i,-] là điểm lớn nhất khi chọn trong giới hạn i số đầu và dấu cuối cùng là '-'
==========
Cơ sở
F[0,1]:=0;
F[0,2]:=0;
f[i, +] = max(f[i - 1, -] + a, f[i - 1, +])
f[i, -] = max(f[i - 1, +] - a, f[i - 1, -])
Kq là max(f[n, +], f[n, -])

Mã:

Var n:longint; A:array[0..1000001] Of Longint; F:array[0..1000001,1..2] Of int64; Procedure Init; Var i:Longint; Begin Readln(n); For i:=1 to n do read(a[i]); writeln; F[0,1]:=0; F[0,2]:=0; End; Function Max(a,b:Longint):Longint; Begin If a>b then max:=a else max:=b; End; Procedure Install; Var i,j:Longint; Begin For i:=1 to n do For j:=1 to 2 do If j=1 then F[i,j]:=Max(F[i-1,j],F[i-1,2]+A[i]) Else F[i,j]:=Max(F[i-1,j],F[i-1,1]-A[i]); Writeln(Max(F[n,1],F[n,2])); End; BEGIN Init; Install; readln end.

lamdetien36 · 20 Tháng bảy 2013

Cho em hỏi tí. "Quy hoạch động trạng thái" là gì vậy mấy anh ?

thienvamai · 21 Tháng bảy 2013

là quy hoạch động theo trạng thái :v

lamdetien36 · 27 Tháng tám 2013

Cho em góp 1 bài cơ bản cho vui

Đề bài:
Đếm số cách phân tích số nguyên dương N (N \leq [TEX]10^5[/TEX]) thành tổng các số nguyên dương không vượt quá N. Do kết quả rất lớn nên chỉ cần lấy phần dư của kết quả khi chia [TEX]10^9[/TEX] (đây là bài KTUAN trên SPOJ)
Ví dụ: N = 5 thì có 7 cách:

Mã:

5 = 1 + 1 + 1 + 1 + 1
5 = 1 + 1 + 1 + 2
5 = 1 + 1 + 3
5 = 1 + 2 + 2
5 = 1 + 4
5 = 2 + 3
5 = 5

Cách giải:
Có nhiều cách để giải bài này, có thể liệt kê tất cả các cách phân tích bằng PP sinh hoặc đệ quy quay lui rồi đếm số kết quả. Ở đây em chỉ nói về cách giải QHĐ.
Cách 1:
Gọi F[i, j] là số cách phân tích i thành tổng các số không vượt quá j.
Kết quả của bài toán sẽ là F[N, N].
Cơ sở QHĐ:

Mã:

F[0, 0] = 1
F[i, 0] = 0 với 1 <= i <= N

Công thức truy hồi:

Mã:

F[i, j] = F[i, j - 1] + F[i - j, j] nếu i >= j
F[i, j] = F[i, j - 1] nếu i < j

Độ phức tạp: O(N^2), bộ nhớ sử dụng là O(N^2).
Có thể cải tiến bộ nhớ sử dụng xuống O(2N), hoặc tốt hơn nữa là O(N).
Cách 2:
Tính theo công thức này:

$85d2425090db971709020599b2e5ff0e.png$

Hoặc viết dễ hiểu hơn là:

$43ece82da690519129ca823eb824f391.png$

Gọi F là số cách phân tích số i.
Kết quả của bài toán là F[N].
Cơ sở QHĐ:

Mã:

F[0]=1

Công thức truy hồi:

Mã:

F[i]=F[i - 1] + F[i - 2] - F[i - 5] - F[i - 7] +....

Trong đó các số 1, 2, 5, 7, ... gọi là generalized pentagonal numbers (không biết dịch thế nào @@) được tính theo công thức

$cda291a091870cd70e74acc97bc407b3.png$
với k = 1, -1, 2, -2, 3, -3...
Đô phức tạp của cách làm này vào khoảng O(518N) (vì k chỉ chạy tới 259 hoặc -259 là hết, chạy quá thì sẽ lớn hơn [TEX]10^5[/TEX])

Cách này có cài ngu cũng chỉ chạy test max mất 0.4s. Tuy nhiên có thể tối ưu để nhanh hơn nữa.
Thứ nhất, hạn chế dùng phép MOD.
Thứ hai, hạn chế dùng IF.
Thứ ba, phải biết tận dụng INLINE )
Thứ tư, chú ý N = 0 thì kết quả là 0 (vì cái này mà em WA chục lần ) )
Và vài thứ nữa...
Đó là kinh nghiệm của em sau khi AC bài KTUAN với time nhanh thứ 1 VN

thienvamai · 27 Tháng tám 2013

Mấy bài kiểu KTUAN rất khó chịu, ai tra đc cái nghiên toán thì làm đc, ai ko tra ra đc thì ko làm đc, mình vừa đọc cái trên wiki mới AC đc

lamdetien36 · 27 Tháng tám 2013

thienvamai said:
Mấy bài kiểu KTUAN rất khó chịu, ai tra đc cái nghiên toán thì làm đc, ai ko tra ra đc thì ko làm đc, mình vừa đọc cái trên wiki mới AC đc

Anh lập cái topic mấy cái kiến thức về toán đi anh. Tổng hợp mấy cái cần thiết ấy. Em lười đọc tiếng Anh quá

Số catalan, phi, ..... đọc TA em không hiểu gì hết

Bài KTUAN sau khi nộp bài mấy chục lần em mới phát hiện ra là có khoảng 3 test trong khoảng (99300 .. 100000)

lamdetien36 · 27 Tháng tám 2013

Em góp thêm bài nữa

Đề bài:
Cho dãy A gồm N số nguyên. Tìm đoạn con (các phần tử liên tiếp) có tổng lớn nhất.
Giới hạn: N \leq 100000.
Ví dụ: A = (2, 3, 4, -2)
KQ là (2, 3, 4) với tổng là 9.

Cách giải:
Gọi F là tổng lớn nhất trong đoạn A[1..i] (có thể không chứa A)
Để tính được F ta dùng thêm 1 mảng phụ F2 với ý nghĩa: F2 là tổng lớn nhất trong đoạn A[1..i] có chứa A
Cơ sở QHĐ:

Mã:

F[0]=0 F2[0] = 0

Công thức truy hồi:

Mã:

F2[i] = Max(F2[i - 1] + A[i], A[i]) F[i] = Max(F[i - 1], F2[i])

Giải thích Công thức truy hồi:

Xét phần tử A
Nếu chọn A vào đoạn con lớn nhất trong đoạn A[1..i] thì F = F2 (theo định nghĩa của mảng F2)
Nếu không chọn A thì đoạn con lớn nhất trong đoạn A[1..i] chuyển thành đoạn con lớn nhất trong đoạn A[1..i-1], hay F = F[i - 1]
Cần chọn F max nên CT là F = Max(F2, F[i - 1]).

Tính F2.
Nếu chọn phần tử A[i-1] vào đoạn con lớn nhất có chứa A trong đoạn A[1..i] thì F2 = F2[i - 1] + A
Nếu không chọn A[i - 1], để thoả mãn tính chất là đoạn gồm các phần tử liên tiếp, ta chỉ có thể chọn phần tử A, tức là F2 = A.
Do đó F2 = Max(F2[i - 1] + A, A)

Bấm để xem đầy đủ nội dung ...

Truy vết:

Ta dựa vào quan hệ giữa F[i - 1] và F2 để tìm ra phần tử cuối của đoạn con cần tìm. Sau đó duyệt lui về 1 cho tới khi nào đạt được tổng lớn nhất (F[N])

Bấm để xem đầy đủ nội dung ...

Độ phức tạp: O(N).

Code hoàn chỉnh:

Mã:

{$MODE DELPHI} uses Math; var A, F1, F2, res: array [0..100] of integer; N, i, k, S: integer; begin write('Nhap N: '); readln(N); for i := 1 to N do begin write(' A[', i : 2, '] = '); read(A[i]); end; F1[1] := A[1]; F2[1] := A[1]; for i := 2 to N do begin F2[i] := Max(A[i], A[i] + F2[i - 1]); F1[i] := Max(F1[i - 1], F2[i]); end; writeln('Tong Lon Nhat: ', F1[N]); (* Truy vet *) k := 0; i := N; while F1[i - 1] > F2[i] do i := i - 1; S := 0; while S < F1[N] do begin k := k + 1; S := S + A[i]; res[k] := A[i]; i := i - 1; end; write('Doan Con La: ('); for i := k downto 2 do write(res[i], '; '); write(res[1], ')'); end.

thienvamai · 28 Tháng tám 2013

Thuật tóan kadane thì chỉ cần lưu 2 biến để chạy thôi, cấn gì 2 mảng

lamdetien36 · 28 Tháng tám 2013

thienvamai said:
Thuật tóan kadane thì chỉ cần lưu 2 biến để chạy thôi, cấn gì 2 mảng

Thì tại em thấy dùng mảng nó dễ giải thích CTTH hơn

thiennu274 · 29 Tháng tám 2013

Ai tìm tiếp em CTTH bài này với!!! Tìm mãi không ra !!!
Cho dãy số nguyên không âm a1,a2,...an. Người ta tiến hành chọn ra 2 chỉ số i,j sao cho 1<=i,j<=n và xóa khỏi dãy 2 số ai,aj để tổng giá trị các số còn lại trong dãy số là số chẵn.
Yêu cầu: Đếm số lượng cách chọn 2 chỉ số i,j thỏa mãn. Hai cách chọn khác nhau nếu tồn tại một chỉ số khác nhau
Input
Dòng 1: chứa số nguyên n (n<=[TEX]10^6[/TEX]
Dòng 2: chứa n số nguyên không âm a1,a2,...an (ai<=[TEX]10^9[/TEX] )
Output
Số cách chọn 2 chỉ số thỏa mãn

mikelhpdatke · 29 Tháng tám 2013

Có 1 cách:

Xét tổng từ a1 -> an, gọi là S

+ Nếu S chẵn, tìm chia ra dãy thành 2 nhóm. Nhóm 1 gồm các sổ lẻ, đếm số cặp. Nhóm 2 tương tự -> KQ.
+ Nếu S lẻ, cũng chia ra thành 2 nhóm. Lấy 1 số nhóm 1 ghép vs 1 số nhóm 2 là được 1 cặp,.. -> KQ

thiennu274 · 30 Tháng tám 2013

mikelhpdatke said:
Có 1 cách:

Xét tổng từ a1 -> an, gọi là S

+ Nếu S chẵn, tìm chia ra dãy thành 2 nhóm. Nhóm 1 gồm các sổ lẻ, đếm số cặp. Nhóm 2 tương tự -> KQ.
+ Nếu S lẻ, cũng chia ra thành 2 nhóm. Lấy 1 số nhóm 1 ghép vs 1 số nhóm 2 là được 1 cặp,.. -> KQ

Mình làm ý tưởng này rồi. Nhưng không thử test lớn được!!!
Mặc dù chỉ lấy ai mod 2 thoi!!! Chỉ xét tính chẳn lẻ nhưng số lớn vẫn không làm được @@

lamdetien36 · 30 Tháng tám 2013

thiennu274 said:
Mình làm ý tưởng này rồi. Nhưng không thử test lớn được!!!
Mặc dù chỉ lấy ai mod 2 thoi!!! Chỉ xét tính chẳn lẻ nhưng số lớn vẫn không làm được @@

Chị nói ko thử test lớn được là sao. Tức là chạy quá lâu hay là tràn số

Tìm kiếm

Tìm kiếm

Tin học Chuyên đề quy hoạch động

11thanhkhoeo

11thanhkhoeo

mikelhpdatke

11thanhkhoeo

mikelhpdatke

mikelhpdatke

11thanhkhoeo

mikelhpdatke

lamdetien36

thienvamai

lamdetien36

thienvamai

lamdetien36

lamdetien36

thienvamai

lamdetien36

thiennu274

mikelhpdatke

thiennu274

lamdetien36