- 28 Tháng một 2016
- 3,897
- 1
- 8,081
- 939
- Yên Bái
- THPT Lê Quý Đôn <3
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chào cả nhà, đây là một phút ngẫu hứng của chị, không lên kế hoạch trước mà là chiều nay khi đang lượn lờ qua diễn đàn gặp một thành viên khá là ham học @boywwalkman đang có nhu cầu tìm hiểu rõ và chuyên sâu về dạng bài tập mạch cầu nên chị quyết định lên luôn cho nóng  hihi
hihi
Mong rằng điều chị sắp trình bày dưới đây sẽ có ý nghĩa với một số bạn, chúc mọi người có một buổi tối vui vẻ, học tập và làm việc thật sự hiệu quả.
Chuyên đề gồm các phần:
1, Nêu lý thuyết và chứng minh
2, Các bài tập vận dụng
3, Loading
Trước đó thì mọi người hãy xem qua các Topic này của chị nhé:
[Vật lý 9] Chuyên đề bồi dưỡng HSG
[Vật lý] Hướng dẫn kĩ năng dò mạch điện
Rồi Ok, không để mọi người chờ lâu hơn nữa chúng ta đi ngay vào phần đầu tiên nhé!
I, Nhận dạng
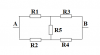
Mạch cầu có dạng như hình dưới:
Trong đó:
Mạch cầu gồm 2 dạng:
a, Mạch cầu cân bằng
Đây cũng chính là phần chính của nội dung lý thuyết này. Chúng ta sẽ chứng minh "Với mạch điện có dạng như trên nếu [imath]I_5=0[/imath] thì ta có công thức: [imath]\dfrac{R_1}{R_2}=\dfrac{R_3}{R_4}[/imath]và ngược lại"
I, Chứng minh theo chiều thuận
Phần này khá đơn giản thôi
Có [imath]I_5=0[/imath] mạch điện trên tương đương: [imath](R_1//R_2)nt(R_3//R_4)[/imath]
Khi đó: [imath]\left\{\begin{matrix} I_1=I_3;I_2=I_4\\ U_1=U_2;U_3=U_4 \end{matrix}\right.[/imath]
[imath]\Rightarrow \left\{\begin{matrix} I_1R_1=I_2R_2\\ I_3R_3=I_4R_4 \end{matrix}\right.\Rightarrow \dfrac{R_1}{R_3}=\dfrac{R_2}{R_4}\Leftrightarrow \dfrac{R_1}{R_2}=\dfrac{R_3}{R_4} (dpcm)[/imath]
II, Chứng minh theo chiều nghịch
Ta có: [imath]\dfrac{R_1}{R_2}=\dfrac{R_3}{R_4}=n\Rightarrow \left\{\begin{matrix} R_1=nR_2\\ R_3=nR_4 \end{matrix}\right.[/imath]
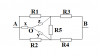
Chúng ta sẽ biến đổi mạch tam giác thành mạch sao, cụ thể như hình:
Khi đó:
[imath]\left\{\begin{matrix} z=\dfrac{R_1R_5}{R_1+R_2+R_5}\\ y=\dfrac{R_2R_5}{R_1+R_2+R_5} \end{matrix}\right.[/imath]
(Tại sao có điều này thì xem ở topic hướng dẫn dò mạch chị có hướng dẫn rồi nhé)
Mạch lúc này trở thành: [imath]xnt[(zntR_3)//(yntR_4)][/imath]
Ta có hệ thức:
[imath]U_3=\dfrac{U_{OB}R_3}{z+R_3}=\dfrac{U_{OB}.R_3(R_1+R_2+R_5)}{R_1R_5+R_3(R_1+R_2+R_5)}=\dfrac{U_{OB}.n.R_4(R_1+R_2+R_5)}{nR_2R_5+n.R_4(R_1+R_2+R_5)}=\dfrac{U_{OB}.R_4(R_1+R_2+R_5)}{R_2R_5+R_4(R_1+R_2+R_5)}[/imath]
Mà : [imath]U_4=\dfrac{U_{OB}R_4}{y+R_4}=\dfrac{U_{OB}.R_4(R_1+R_2+R_5)}{R_2R_5+R_4(R_1+R_2+R_5)}[/imath]
[imath]\Rightarrow U_3=U_4\Rightarrow I_5=0(dpcm)[/imath]
Vậy là phần 1 đã xong, hẹn mọi người ở lần lên bài tiếp theo!
Mong rằng điều chị sắp trình bày dưới đây sẽ có ý nghĩa với một số bạn, chúc mọi người có một buổi tối vui vẻ, học tập và làm việc thật sự hiệu quả.
Chuyên đề gồm các phần:
1, Nêu lý thuyết và chứng minh
2, Các bài tập vận dụng
3, Loading
Trước đó thì mọi người hãy xem qua các Topic này của chị nhé:
[Vật lý 9] Chuyên đề bồi dưỡng HSG
[Vật lý] Hướng dẫn kĩ năng dò mạch điện
Rồi Ok, không để mọi người chờ lâu hơn nữa chúng ta đi ngay vào phần đầu tiên nhé!
Phần 1: Nêu lý thuyết và chứng minh
A, Lý thuyếtI, Nhận dạng
Mạch cầu có dạng như hình dưới:
Trong đó:
- [imath]R_1,R_2,R_3,R_4[/imath] được gọi là các điện trở cạnh
- [imath]R_5[/imath] được gọi là điện trở gánh
Mạch cầu gồm 2 dạng:
- Mạch cầu cân bằng
- Mạch cầu không cân bằng:
- Mạch cầu đủ (tổng quát)
- Mạch cầu khuyết
a, Mạch cầu cân bằng
- Khi đặt một hiệu điện thế [imath]U_{AB}=0[/imath] thì ta nhận thấy [imath]I_5=0[/imath]
- Khi đó mạch cầu cân bằng và có đặc điểm: [imath]\left\{\begin{matrix} I_1=I_3;I_2=I_4\\ U_1=U_2;U_3=U_4 \end{matrix}\right.[/imath]
- Điều này sẽ dẫn đến hệ quả: [imath]\dfrac{R_1}{R_2}=\dfrac{R_3}{R_4}[/imath] (*)
- Khi đặt một hiệu điện thế [imath]U_{AB}=0[/imath] thì ta nhận thấy [imath]I_5[/imath] khác 0$
- Khi mạch cầu không có đủ 5 điện trở thì gọi là mạch cầu khuyết
Đây cũng chính là phần chính của nội dung lý thuyết này. Chúng ta sẽ chứng minh "Với mạch điện có dạng như trên nếu [imath]I_5=0[/imath] thì ta có công thức: [imath]\dfrac{R_1}{R_2}=\dfrac{R_3}{R_4}[/imath]và ngược lại"
I, Chứng minh theo chiều thuận
Phần này khá đơn giản thôi
Có [imath]I_5=0[/imath] mạch điện trên tương đương: [imath](R_1//R_2)nt(R_3//R_4)[/imath]
Khi đó: [imath]\left\{\begin{matrix} I_1=I_3;I_2=I_4\\ U_1=U_2;U_3=U_4 \end{matrix}\right.[/imath]
[imath]\Rightarrow \left\{\begin{matrix} I_1R_1=I_2R_2\\ I_3R_3=I_4R_4 \end{matrix}\right.\Rightarrow \dfrac{R_1}{R_3}=\dfrac{R_2}{R_4}\Leftrightarrow \dfrac{R_1}{R_2}=\dfrac{R_3}{R_4} (dpcm)[/imath]
II, Chứng minh theo chiều nghịch
Ta có: [imath]\dfrac{R_1}{R_2}=\dfrac{R_3}{R_4}=n\Rightarrow \left\{\begin{matrix} R_1=nR_2\\ R_3=nR_4 \end{matrix}\right.[/imath]
Chúng ta sẽ biến đổi mạch tam giác thành mạch sao, cụ thể như hình:
Khi đó:
[imath]\left\{\begin{matrix} z=\dfrac{R_1R_5}{R_1+R_2+R_5}\\ y=\dfrac{R_2R_5}{R_1+R_2+R_5} \end{matrix}\right.[/imath]
(Tại sao có điều này thì xem ở topic hướng dẫn dò mạch chị có hướng dẫn rồi nhé)
Mạch lúc này trở thành: [imath]xnt[(zntR_3)//(yntR_4)][/imath]
Ta có hệ thức:
[imath]U_3=\dfrac{U_{OB}R_3}{z+R_3}=\dfrac{U_{OB}.R_3(R_1+R_2+R_5)}{R_1R_5+R_3(R_1+R_2+R_5)}=\dfrac{U_{OB}.n.R_4(R_1+R_2+R_5)}{nR_2R_5+n.R_4(R_1+R_2+R_5)}=\dfrac{U_{OB}.R_4(R_1+R_2+R_5)}{R_2R_5+R_4(R_1+R_2+R_5)}[/imath]
Mà : [imath]U_4=\dfrac{U_{OB}R_4}{y+R_4}=\dfrac{U_{OB}.R_4(R_1+R_2+R_5)}{R_2R_5+R_4(R_1+R_2+R_5)}[/imath]
[imath]\Rightarrow U_3=U_4\Rightarrow I_5=0(dpcm)[/imath]
Vậy là phần 1 đã xong, hẹn mọi người ở lần lên bài tiếp theo!