Giovanni Ceva (ngày 07 tháng 12 1647 - 15 tháng 6 1734) là một nhà toán học người Ý được biết đến rộng rãi để chứng minh định lý Ceva trong hình học cơ bản. Anh trai của ông, Tommaso Ceva cũng là một nhà thơ nổi tiếng và nhà toán học.
Ceva theo học tại một trường đại học Dòng Tên ở Milan. Sau này trong cuộc sống của mình, ông học tại Đại học Pisa, nơi ông sau đó trở thành một giáo sư. Vào năm 1686, tuy nhiên, ông đã được chỉ định là Giáo sư Toán học tại Đại học Mantua và làm việc ở đó cho phần còn lại của cuộc đời mình.
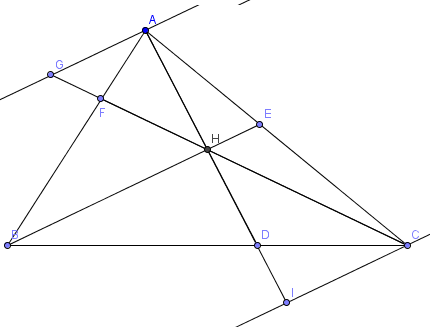
Ceva nghiên cứu hình học cho hầu hết của cuộc sống lâu dài của mình. Vào năm 1678, ông xuất bản một định lý nổi tiếng về hình học tổng hợp trong một hình tam giác được gọi là Định lý Ceva. Định lý nói rằng nếu ba đoạn đường được rút ra từ các đỉnh của một hình tam giác với các cạnh đối diện, sau đó các phân đoạn đường ba là đồng thời nếu và chỉ nếu, tích của các tỷ lệ của các phân đoạn đường mới được tạo ra trên mỗi bên của tam giác bằng một. Ông đã xuất bản định lý mới này trong De lineis rectis.
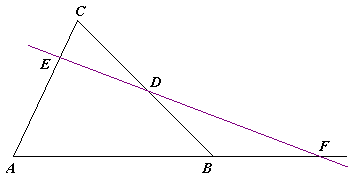
Ceva không chỉ được công bố định lý riêng của mình, nhưng ông cũng khám phá và công bố định lý Menelaus. Ông đã xuất bản Opuscula Mathematica trong năm 1682 và Geometria Motus năm 1692, là tốt. Trong Geometria Motus, ông dự đoán các tính toán vô cùng. Cuối cùng, Ceva viết De Re Nummeraria năm 1711, đó là một trong những cuốn sách đầu tiên về kinh tế toán học.
Giovanni Ceva cũng nghiên cứu các ứng dụng của cơ học và tĩnh với các hệ thống hình học. Tại một thời điểm, tuy nhiên, ông không chính xác giải quyết các thời kỳ dao động của con lắc là hai trong cùng một tỷ lệ như độ dài của họ, nhưng sau đó ông nhận ra và sửa chữa các lỗi. Ceva cũng làm việc về thủy lực. Năm 1728, ông xuất bản Opus hydrostaticum mà thảo luận về công việc của mình trong hệ thống thủy lực. Trong thực tế, ông đã sử dụng kiến thức của ông về hệ thống thủy lực để ngăn chặn một dự án từ chuyển Reno sông xuống sông Po.