(Đi tìm lời giải trên mạng :v)
Gọi các điểm như sau:
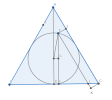
Đặt [imath]EF=x,EH=y,EJ=z,AD=h[/imath] thì ta cần chứng minh [imath]x^2+y^2+z^2[/imath] không đổi.
Ta có [imath]ID=IE=GF=\dfrac{h}{3} \Rightarrow EG=x-\dfrac{h}{3}[/imath]
[imath]DC=\dfrac{AD}{\sqrt{3}}=\dfrac{h}{\sqrt{3}}[/imath]
[imath]FL=\dfrac{EF}{\sqrt{3}}=\dfrac{x}{\sqrt{3}}[/imath]
[imath]CL=\dfrac{2}{\sqrt{3}}CK=\dfrac{2EJ}{\sqrt{3}}=\dfrac{2z}{\sqrt{3}}[/imath]
[imath]\Rightarrow IG=DF=DC-FL-LC=\dfrac{h-x-2z}{\sqrt{3}}[/imath]
Áp dụng định lý Pythagoras cho [imath]\Delta IGE[/imath] ta được:
[imath]\dfrac{(h-x-2z)^2}{3}+(x-\dfrac{h}{3})^2=\dfrac{h}{9}^2[/imath]
[imath]\Rightarrow x^2+z^2=h(x+z)-xz-\dfrac{h^2}{4}[/imath]
Tương tự ta cũng chứng minh được [imath]x^2+y^2=h(x+y)-xy-\dfrac{h^2}{4}[/imath]
[imath]\Rightarrow 2x^2+y^2+z^2=h(2x+y+z)-x(y+z)-\dfrac{h^2}{2}[/imath]
Mặt khác, ta dễ chứng minh được [imath]x+y+z=EF+EH+EJ=h[/imath]
[imath]\Rightarrow 2x^2+y^2+z^2=h(x+h)-x(h-x)-\dfrac{h^2}{2}=x^2+\dfrac{h^2}{2}[/imath]
[imath]\Rightarrow x^2+y^2+z^2=\dfrac{h^2}{2}[/imath] không đổi.
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé. Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại topic này nha
Trọn bộ kiến thức học tốt TẤT CẢ các môn học
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
