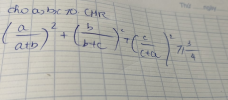Nguyễn Chi XuyênĐặt [imath]\dfrac{b}{a} =x; \cdots[/imath] thì [imath]xyz=1[/imath]
Giả sử [imath]x\geq y\geq z \Rightarrow z\leq 1 \Rightarrow xy \geq 1[/imath]
BDT trở thành: [imath]P= \dfrac{1}{(1+x)^2} + \dfrac{1}{(1+y)^2} +\dfrac{1}{(1+z)^2} \geq \dfrac{3}{4}[/imath]
Sau đó em chứng minh BĐT phụ: [imath]\dfrac{1}{(1+x)^2} + \dfrac{1}{(1+y)^2} \geq \dfrac{1}{2(1+x^2)} + \dfrac{1}{2(1+y^2)} \geq \dfrac{1}{1+xy}[/imath] với [imath]xy\geq 1[/imath]
Áp dụng luôn ta có: [imath]P \geq \dfrac{1}{1+xy} + \dfrac{1}{(1+z)^2} = \dfrac{z}{z+1} + \dfrac{1}{(z+1)^2} = \dfrac{z^2 + z+1}{(z+1)^2}[/imath]
[imath]\Rightarrow P -\dfrac{3}{4} = \dfrac{(z-1)^2 }{(z+1)^2} \geq 0[/imath]
Nên bdt được chứng minh.
Dấu = xảy ra tại [imath]x=y=z=1[/imath] hay [imath]a=b=c[/imath]
Ngoài ra mời em tham khảo [Lý thuyết] Chuyên đề HSG : Bất đẳng thức
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
