- 23 Tháng mười một 2019
- 4,605
- 12,668
- 1,021
- Nam Định
- In the sky
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Giúp em với ạ:
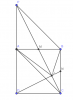
Bài 6: Cho hình vuông ABCD, M là là trung điểm cạnh AB, P là giao điểm của hai tia CM và
DA.
a) Chứng minh tứ giác APBC là hình bình hành và tứ giác BCDP là hình thang vuông.
b) Chứng minh 2S BCDP = 3S APBC .
c) Gọi N là trung điểm BC,Q là giao điểm của DN và CM..Chứng minh AQ = AB.
Bài 6: Cho hình vuông ABCD, M là là trung điểm cạnh AB, P là giao điểm của hai tia CM và
DA.
a) Chứng minh tứ giác APBC là hình bình hành và tứ giác BCDP là hình thang vuông.
b) Chứng minh 2S BCDP = 3S APBC .
c) Gọi N là trung điểm BC,Q là giao điểm của DN và CM..Chứng minh AQ = AB.