[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Có một chứng minh Tiên đề Euclid. Các bạn xem nhé !
ĐỊNH LÍ EUCLID
Định lí Euclid: Qua một điểm ở ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.(Tiên đề Euclid)
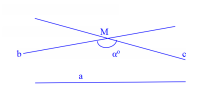
Chứng minh:
Giả sử qua M có hai đường thẳng b và c cùng song song với a.
Vì b//a nên đường thẳng a phải nằm trong một nửa mặt phẳng nào đó có bờ là b. Tương tự do c//a nên đường thẳng a phải nằm trong một nửa mặt phẳng nào đó có bờ là c. Từ đó a nằm trong phần chung của hai nửa mặt phẳng này do đó a nằm trong góc bMc do hai đường thẳng b,c cắt nhau tại M tạo ra.
Gọi α là số đo (độ) của góc bMc (0 < α < 180). Ta có: Miền góc bMc chiếm α/180 phần của nửa mặt phẳng vì bMc = α độ = α.1độ = α.(1/180).180o = α.(1/180).nmp = (α/180)nmp, và có α/180 < 1 vì α < 180.
Do a nằm trong góc bMc nên nửa mặt phẳng bờ a không chứa b và c sẽ nằm trọn trong góc bMc. Như vậy nmp(a,M) ⸦ bMc ⇒ nmp(a,M) - bMc = ∅ ⇒ nmp - (α/180)nmp = ∅ ⇒ [1-(α/180)]nmp = ∅ ⇒ γ.nmp = ∅ (với 0<γ<1) → Vô lí.
Vậy qua M chỉ có duy nhất một đường thẳng m song song với a mà thôi.□
ĐỊNH LÍ EUCLID
Định lí Euclid: Qua một điểm ở ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.(Tiên đề Euclid)
Chứng minh:
Giả sử qua M có hai đường thẳng b và c cùng song song với a.
Vì b//a nên đường thẳng a phải nằm trong một nửa mặt phẳng nào đó có bờ là b. Tương tự do c//a nên đường thẳng a phải nằm trong một nửa mặt phẳng nào đó có bờ là c. Từ đó a nằm trong phần chung của hai nửa mặt phẳng này do đó a nằm trong góc bMc do hai đường thẳng b,c cắt nhau tại M tạo ra.
Gọi α là số đo (độ) của góc bMc (0 < α < 180). Ta có: Miền góc bMc chiếm α/180 phần của nửa mặt phẳng vì bMc = α độ = α.1độ = α.(1/180).180o = α.(1/180).nmp = (α/180)nmp, và có α/180 < 1 vì α < 180.
Do a nằm trong góc bMc nên nửa mặt phẳng bờ a không chứa b và c sẽ nằm trọn trong góc bMc. Như vậy nmp(a,
Vậy qua M chỉ có duy nhất một đường thẳng m song song với a mà thôi.□
