[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
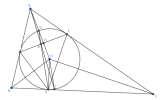
Cho điểm [imath]A[/imath] cố định nằm ngoài đường tròn [imath](O)[/imath]. Kẻ các tiếp tuyến [imath]AE,AF[/imath] của [imath](O)[/imath]. Điểm [imath]D[/imath] di động trên cung lớn [imath]EF[/imath] sao cho [imath]DE<DF[/imath], [imath]D[/imath] không trùng [imath]E[/imath] và tiếp tuyến tại [imath]D[/imath] của [imath](O)[/imath] cắt các tia [imath]AE,AF[/imath] lần lượt tại [imath]B,C[/imath].
a) Gọi [imath]M,N[/imath] lần lượt là giao điểm của đường thẳng [imath]EF[/imath] với các đường thẳng [imath]OB,OC[/imath]. Chứng minh [imath]BMNC[/imath] nội tiếp đường tròn,
b) Vẽ tia phân giác [imath]DK[/imath] của [imath]\widehat{EDF}[/imath] và tia phân giác [imath]OI[/imath] của [imath]\widehat{BOC}[/imath] với [imath]K[/imath] thuộc [imath]EF[/imath] và [imath]I[/imath] thuộc [imath]BC[/imath]. Chứng minh [imath]OI \parallel DK[/imath]
c) Chứng minh đường thẳng [imath]IK[/imath] đi qua 1 điểm cố định.
@Mộc Nhãn @kido2006 @HT2k02(Re-kido) mọi người giúp e ý c với ạ
Cho [imath]\Delta ABC[/imath] nhọn nội tiếp đường tròn [imath](O)[/imath], trực tâm [imath]H[/imath], [imath]AH[/imath] cắt [imath](O)[/imath] tại [imath]Q[/imath], vẽ đường kính [imath]AD[/imath], phân giác [imath]\widehat{BAC}[/imath] cắt [imath]HD[/imath] tại [imath]P[/imath]. Đường tròn đường kính [imath]AP[/imath] cắt [imath]AB,AC[/imath] tại [imath]E,F[/imath].
a) Chứng minh [imath]BCDQ[/imath] là hình thang cân.
b) Chứng minh [imath]E,H,F[/imath] thẳng hàng.
còn câu này nhờ mọi người giúp ý b ak
a) Gọi [imath]M,N[/imath] lần lượt là giao điểm của đường thẳng [imath]EF[/imath] với các đường thẳng [imath]OB,OC[/imath]. Chứng minh [imath]BMNC[/imath] nội tiếp đường tròn,
b) Vẽ tia phân giác [imath]DK[/imath] của [imath]\widehat{EDF}[/imath] và tia phân giác [imath]OI[/imath] của [imath]\widehat{BOC}[/imath] với [imath]K[/imath] thuộc [imath]EF[/imath] và [imath]I[/imath] thuộc [imath]BC[/imath]. Chứng minh [imath]OI \parallel DK[/imath]
c) Chứng minh đường thẳng [imath]IK[/imath] đi qua 1 điểm cố định.
@Mộc Nhãn @kido2006 @HT2k02(Re-kido) mọi người giúp e ý c với ạ
Cho [imath]\Delta ABC[/imath] nhọn nội tiếp đường tròn [imath](O)[/imath], trực tâm [imath]H[/imath], [imath]AH[/imath] cắt [imath](O)[/imath] tại [imath]Q[/imath], vẽ đường kính [imath]AD[/imath], phân giác [imath]\widehat{BAC}[/imath] cắt [imath]HD[/imath] tại [imath]P[/imath]. Đường tròn đường kính [imath]AP[/imath] cắt [imath]AB,AC[/imath] tại [imath]E,F[/imath].
a) Chứng minh [imath]BCDQ[/imath] là hình thang cân.
b) Chứng minh [imath]E,H,F[/imath] thẳng hàng.
còn câu này nhờ mọi người giúp ý b ak
Attachments
Last edited by a moderator:
